题目内容
【题目】如图1，抛物线
与
轴交于点
、
两点，与
轴交于点
．
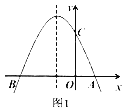
（1）求该抛物线的解析式；
（2）在该抛物线的对称轴上是否存在点
，使得
的周长最小？若存在，求出点的坐标；若不存在，请说明理由．
【答案】（1）
；（2）存在，
【解析】
（1）利用待定系数法求出抛物线解析式即可；
（2）由题知A、B两点关于抛物线的对称x=-1对称，直线BC与x=-1的交点即为Q点，此时△AQC周长最小，首先求出直线BC的解析式，进而得出Q点坐标即为
的解，即可得出答案．
(1)将A(1,0),B(3,0)代
中得
，
∴解得：
，
∴抛物线解析式为：；
（2）)存在，
理由如下：由题知A. B两点关于抛物线的对称轴x=1对称，
∴直线BC与x=1的交点即为Q点，此时△AQC周长最小
∵，
∵C的坐标为：(0,3),B(3,0)，设直线BC解析式为：y=kx+d，
∴
，
解得：
，
∴直线BC解析式为：y=x+3；
Q点坐标即为的解，
∴
，
∴Q(1,2).
练习册系列答案
相关题目
【题目】已知二次函数
的
与
的部分对应值如下表：
| -1 | 0 | 1 | 3 |
| -3 | 1 | 3 | 1 |
下列结论：①抛物线的开口向下；②其图象的对称轴为
；③当
时，函数值
随
的增大而增大；④方程
有一个根大于4．其中正确的结论有（ ）
A．1个 B．2个 C.3个 D．4个
