题目内容
20.如图,是用棋子摆成的图案,摆第1个图案需要7枚棋子,摆第2个图案需要19枚棋子,按照这样的方式摆下去,则摆第4个图案需要61枚棋子,摆第n个图案需要3n2+3n+1枚棋子.
分析 依次求得n=1,2,3,…,图案需要的棋子枚数.再根据规律以此类推,可得出第n个图案需要的棋子枚数,进一步代入求得答案即可.
解答 解:∵n=1时,总数是6+1=7;
n=2时,总数为6×(1+2)+1=19;
n=3时,总数为6×(1+2+3)+1=37枚;
…;
∴n=n时,有6×(1+2+3+…n)+1=6×$\frac{n(n+1)}{2}$+1=3n2+3n+1枚.
∴n=5时,总数为6×(1+2+3+4)+1=61枚.
故答案为:61,3n2+3n+1.
点评 此题考查图形的变化规律,找出图形之间的联系,得出数字之间的运算规律,利用规律解决问题.

练习册系列答案
相关题目
 如图,AB=AC,BD=CE,用无刻度的直尺画出∠A的平分线.
如图,AB=AC,BD=CE,用无刻度的直尺画出∠A的平分线.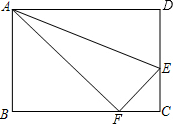 如图,折叠长方形纸片ABCD的一边AD,使点D落在BC边上的点F处,AE为折痕.已知AB=8,BC=10,则EC的长为3.
如图,折叠长方形纸片ABCD的一边AD,使点D落在BC边上的点F处,AE为折痕.已知AB=8,BC=10,则EC的长为3.