题目内容
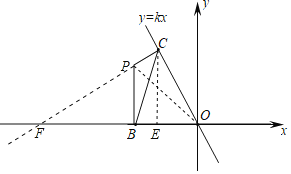
【题目】如图，在平面直角坐标系中，直线y＝kx（k≠0）经过点（m，
m）（m＜0）．线段BC的两个端点分别在x轴与直线y＝kx上滑动（B、C均与原点O不重合），且BC＝
．分别作BP⊥x轴，CP⊥直线y＝kx，直线BP、CP交于点P．经探究，在整个滑动过程中，O、P两点间的距离为定值，则该距离为_____．
【答案】
．
【解析】
如图（见解析），过C作
轴，垂足为E，设
，由条件可知
，根据直角三角的性质可分别表示出CE和BE的长，在
中，可求得
的值，则可求得PO的长，可得出答案.
如图，过点C作轴于点E，延长CP交x轴于点F，连接OP
∵直线
经过点
由勾股定理得
设P点坐标为
（不妨设点P在第二象限，其他同理可求得）
则
在
中，可得
在
中，
在
中，
则
在中，
，由勾股定理可得
则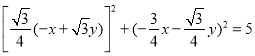
整理得
即O、P两点的距离为定值
故答案为：.
练习册系列答案
相关题目
