题目内容
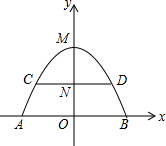如图是抛物线形拱桥，已知水位在AB位置时，水面宽4| 6 |
| 3 |
| A、6 | B、12 | C、18 | D、24 |
考点：二次函数的应用
专题：应用题
分析：已知B、D可得y的解析式，从而求出OM的值．又因为MN=OM-ON，故可求t的值．
解答：解：根据题意设抛物线解析式为：y=ax2+h
又∵B（2
，0），D（2
，3）
∴
，
解得：
，
∴y=-
x2+6
∴M（0，6）即OM=6m
∴MN=OM-ON=3，
则t=
=12（小时）．
答：水过警戒线后12小时淹到拱桥顶．
故选：B．
又∵B（2
| 6 |
| 3 |
∴
|
解得：
|
∴y=-
| 1 |
| 4 |
∴M（0，6）即OM=6m
∴MN=OM-ON=3，
则t=
| MN |
| 0.25 |
答：水过警戒线后12小时淹到拱桥顶．
故选：B．
点评：本题考查二次函数的实际应用．此题为数学建模题，借助二次函数解决实际问题．
练习册系列答案
暑假作业海燕出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
相关题目
下列图形属于平面图形的是（ ）
| A、长方体 | B、圆锥体 |
| C、圆柱体 | D、圆 |
在矩形ABCD中，AE⊥BD，垂足为E，∠DAE=3∠BAE，则∠CBD等于（ ）
| A、22.5° | B、30° |
| C、45° | D、60° |
在下列多项式乘法中，可以用平方差公式计算的是（ ）
| A、（2a-3b）（-2a+3b） |
| B、（-3a+4b）（-4b-3a） |
| C、（a+1）（-a-1） |
| D、（a2-b）（a+b2） |
若代数式
有意义，则实数x的取值范围是（ ）
| ||
| x+1 |
| A、x≠-1 | B、x≥0 |
| C、x＞0 | D、x≤0且x≠-1 |
点P在直线y=-x+4上，并且它的纵坐标是3，那么点P关于x轴的对称点P′的坐标为（ ）
| A、（1，3） |
| B、（1，-3） |
| C、（-1，3） |
| D、（-1，-3） |
下列说法中，正确的是（ ）
| A、若ac=bc，则a=b | ||||
B、若
| ||||
| C、若a2=b2，则a=b | ||||
| D、若|a|=|b|，则a=b |
若⊙O1、⊙O2的直径分别为4和6，圆心距O1O2=2，则⊙O1与⊙O2的位置关系是（ ）
| A、相交 | B、外离 | C、外切 | D、内切 |
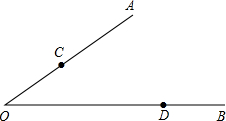画图：如图，已知点C、点D分别在∠AOB的边上，请根据下列语句画出图形：