题目内容
在矩形ABCD中，AE⊥BD，垂足为E，∠DAE=3∠BAE，则∠CBD等于（ ）
| A、22.5° | B、30° |
| C、45° | D、60° |
考点：矩形的性质
专题：
分析：由AE⊥BD和∠DAE=3∠BAE，得∠ABE=67.5°，从而求出∠CBD的度数．
解答：
解：如图，∵AE⊥BD，
∴∠AEB=90°，
∵四边形ABCD是矩形，
∴∠DAB=∠ABC=90°，
∵∠DAE=3∠BAE，
∴∠DAE=67.5°°，∠BAE=22.5°，
∴∠ABE=67.5°，
∴∠CBD=22.5°．
故选A．
解：如图，∵AE⊥BD，∴∠AEB=90°，
∵四边形ABCD是矩形，
∴∠DAB=∠ABC=90°，
∵∠DAE=3∠BAE，
∴∠DAE=67.5°°，∠BAE=22.5°，
∴∠ABE=67.5°，
∴∠CBD=22.5°．
故选A．
点评：本题考查了矩形的四个角都是直角的性质，题目比较典型，难度不大．
练习册系列答案
相关题目
两圆相切，半径分别为4和r，圆心距为5，则r为（ ）
| A、1 | B、9 |
| C、1或9 | D、1＜r＜9 |
下列方程中，是一元一次方程的是（ ）
| A、x-y=1 | ||
| B、y-4=2y | ||
| C、y=3x | ||
D、
|
点M（4，-3）关于原点的对称点在（ ）
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
如果一个两位数的十位数字与个位数字之和为6，差为2，那么这个两位数是（ ）
| A、72 | B、62 | C、52 | D、42 |
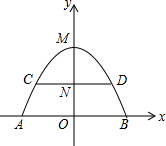如图是抛物线形拱桥，已知水位在AB位置时，水面宽4