题目内容
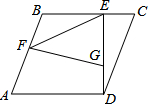 平行四边形ABCD中,DE⊥BC于E,且DE=BC,EG=BE,过G作GF⊥AB于F,连接EF.
平行四边形ABCD中,DE⊥BC于E,且DE=BC,EG=BE,过G作GF⊥AB于F,连接EF.(1)若平行四边形ABCD的面积为9,∠FEB+∠A=90°,且tan∠FEB=
| 1 |
| 3 |
(2)求证:
| 2 |
考点:平行四边形的性质,解直角三角形
专题:几何图形问题,证明题
分析:(1)根据面积求出BC和DE,解直角三角形求出CE,即可求出答案;
(2)过点E作EH⊥GF,EI⊥AB,求出正方形IFHE,推出FI=FH=EH,根据勾股定理和等腰直角三角形求出EF=
FI,即可得出答案.
(2)过点E作EH⊥GF,EI⊥AB,求出正方形IFHE,推出FI=FH=EH,根据勾股定理和等腰直角三角形求出EF=
| 2 |
解答:(1)解:∵DE=BC,平行四边形ABCD的面积为9,
∴BC=DE=3,∠C=∠A,
∵∠FEB+∠A=90°,且tan∠FEB=
,
∴
=
,
∴CE=1,
∴BE=EG=3-1=2,
∴DG=3-2=1;
(2)证明:过点E作EH⊥GF,EI⊥AB,
∵GF⊥AB,
∴∠I=∠IFG=∠FHE=90°,
∴四边形IFHE是矩形,
∴∠IEH=90°,
∵DE⊥BC,
∴∠BED=90°,
∴∠IEB=∠HEG=90°-∠BEH,
在△EIB和△EHG中
∴△EIB≌EHG(AAS),
∴EH=EI,BI=HG,
∴矩形EHFI是正方形,
∴EI=IF=FH=EH,
即EF=
FI,
∴
FE-FB=2FI-FB=FI+BI=FH+HG=FG,
即
FE-FB=FG.
∴BC=DE=3,∠C=∠A,
∵∠FEB+∠A=90°,且tan∠FEB=
| 1 |
| 3 |
∴
| CE |
| DE |
| 1 |
| 3 |
∴CE=1,
∴BE=EG=3-1=2,
∴DG=3-2=1;
(2)证明:过点E作EH⊥GF,EI⊥AB,

∵GF⊥AB,
∴∠I=∠IFG=∠FHE=90°,
∴四边形IFHE是矩形,
∴∠IEH=90°,
∵DE⊥BC,
∴∠BED=90°,
∴∠IEB=∠HEG=90°-∠BEH,
在△EIB和△EHG中
|
∴△EIB≌EHG(AAS),
∴EH=EI,BI=HG,
∴矩形EHFI是正方形,
∴EI=IF=FH=EH,
即EF=
| 2 |
∴
| 2 |
即
| 2 |
点评:本题考查了正方形的性质和判定,平行四边形的性质,解直角三角形,勾股定理等知识点的应用,主要考查学生综合运用定理进行推理的能力,题目综合性比较强,难度偏大.

练习册系列答案
相关题目
一组数据10,9,8.5,8,9.5的极差是( )
| A、0.5 | B、8.5 |
| C、2.5 | D、2 |

 如图△ABC在平面直角坐标系中,若把三角形ABC绕着点O顺时针旋转90°,试解决下列问题:
如图△ABC在平面直角坐标系中,若把三角形ABC绕着点O顺时针旋转90°,试解决下列问题: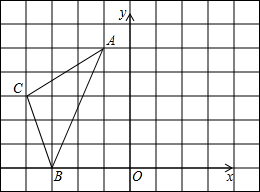 如图,在直角坐标系xOy中,A(-l,5),B(-3,0),C(-4,3).
如图,在直角坐标系xOy中,A(-l,5),B(-3,0),C(-4,3).