题目内容
9.一个直角三角形的直角边的和为14cm,斜边长10cm,求两直角边的长.若设其中一条直角边长为xcm,则另一条直角边长为14-xcm,依题意可列方程为:x2-14x+48=0.分析 首先设出一边长,然后表示出另一条直角边的长,利用勾股定理两直角边的平方和等于斜边的平方即可列出方程.
解答 解:设其中一条直角边长为xcm,则另一条直角边长为(14-x)cm,
根据勾股定理可得,
x2+(14-x)2=102,
即x2-14x+48=0,
故答案为14-x;x2-14x+48=0
点评 本题考查了由实际问题抽象出一元二次方程的知识,解题的关键是掌握勾股定理的知识.

练习册系列答案
相关题目
1.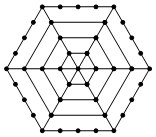 如图,有一个形如六边形的点阵,它的中心是一个点,从内向外算,中心为第一层,第二层每边有两个点,第三层每边有三个点,依此类推.
如图,有一个形如六边形的点阵,它的中心是一个点,从内向外算,中心为第一层,第二层每边有两个点,第三层每边有三个点,依此类推.
(1)填写如表:
(2)写出第n层所对应的总点数:写出n层的六边形点阵的总点数.
 如图,有一个形如六边形的点阵,它的中心是一个点,从内向外算,中心为第一层,第二层每边有两个点,第三层每边有三个点,依此类推.
如图,有一个形如六边形的点阵,它的中心是一个点,从内向外算,中心为第一层,第二层每边有两个点,第三层每边有三个点,依此类推.(1)填写如表:
| 层数 | 1 | 2 | 3 | 4 | 5 | 6 |
| 该层对应的点数 | 1 | 6 | 12 | 18 | 24 | 30 |
| 所有层的总点数 | 1 | 7 | 19 | 37 | 61 | 91 |
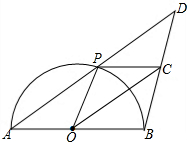 如图,已知半圆O的直径AB=4,点P是半圆上不与点A、B重合的动点,延长AP到点D,使AP=PD,连接BD,点C是BD的中点,连接OP、OC、PC.
如图,已知半圆O的直径AB=4,点P是半圆上不与点A、B重合的动点,延长AP到点D,使AP=PD,连接BD,点C是BD的中点,连接OP、OC、PC.
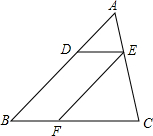 如图,△ABC中,点D、E、F分别在边AB、AC、BC上,且DE∥BC,EF∥AB,DE:BC=1:3,那么EF:AB的值为$\frac{2}{3}$.
如图,△ABC中,点D、E、F分别在边AB、AC、BC上,且DE∥BC,EF∥AB,DE:BC=1:3,那么EF:AB的值为$\frac{2}{3}$.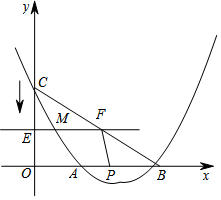 如图,抛物线y=a2+bx+c(a>0)交x轴于A(4,0)、B(8,0)两点,交y轴于点C,且$\frac{OC}{OB}$=$\frac{1}{2}$.
如图,抛物线y=a2+bx+c(a>0)交x轴于A(4,0)、B(8,0)两点,交y轴于点C,且$\frac{OC}{OB}$=$\frac{1}{2}$.