Question

13．如图，在△ABC中，∠ACB=90°，AD平分∠CAB交BC于D，AC=6，BC=8，求S_△ABD．

Answer 1

分析 作DE⊥AB，垂足为E，DE即为D到AB的距离．由角平分线的性质证得DE=DC．在△ABC中，由勾股定理求得AB=10，设CD=x，则DE=CD=x，BD=8-x．AE=AC=6，则BE=4，在Rt△BED中由勾股定理列出x²+4²=（8-x）²，求得x的值，然后根据三角形的面积公式即可得到结论．

解答 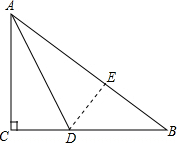解：作DE⊥AB，垂足为E，DE即为D到AB的距离．
又∵∠C=90°，AD平分∠CAB，
∴DE=DC，
在△ABC中，∵∠C=90°，BC=8，AC=6，
∴AB=10，设CD=x，
则DE=CD=x，BD=8-x．
在Rt△ACD与Rt△AED中，∵$\left\{\begin{array}{l}{CD=DE}\\{AD=AD}\end{array}\right.$，
∴Rt△ACD≌Rt△AED（HL），
∴AE=AC=6，∴BE=4，
在Rt△BED中，∵DE²+EB²=DB²，即x²+4²=（8-x）²，
解得：x=3，
∴S_△ABD．=$\frac{1}{2}$AB•DE=$\frac{1}{2}×10×3$=15．

点评 本题考查了角平分线的性质和全等三角形的判定与性质．由已知能够注意到D到AB的距离即为DE长是解决的关键．