Question

6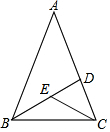．如图，在△ABC中，AB=AC，∠A=36°，BD，CE分别平分∠ABC，∠ACB，若CD=3，则CE等于（　　）

• A． 2
• B． 2.5
• C． 3
• D． 3.5

Answer 1

分析 根据等腰三角形性质和三角形的内角和得到∠ABC=∠ACB=72°，根据角平分线的定义得到∠DBC=∠ACE=36°，根据三角形的内角和得到∠CED=180°-∠ACE-∠BDC=72°，于是得到结论．

解答 解：∵AB=AC，∠A=36°，
∴∠ABC=∠ACB=72°，
∵BD，CE分别平分∠ABC，∠ACB，
∴∠DBC=∠ACE=36°，
∴∠BDC=72°，
∴∠CED=180°-∠ACE-∠BDC=72°，
∴∠CED=∠CDE，
∴CE=CD=3，
故选C．

点评 本题考查了等腰三角形的性质和判定，三角形的内角和，熟练掌握等腰三角形的性质是解题的关键．