题目内容
4.若函数y=(m-1)x|m|是正比例函数,则该函数的图象经过第二、四象限.分析 根据正比例函数定义可得:|m|=1,且m-1≠0,计算出m的值,然后可得解析式,再根据正比例函数的性质可得答案.
解答 解:由题意得:|m|=1,且m-1≠0,
解得:m=-1,
函数解析式为y=-2x,
∵k=-2<0,
∴该函数的图象经过第二、四象限.
故答案为:二、四.
点评 此题主要考查了正比例函数的定义和性质,关键是掌握形如y=kx(k是常数,k≠0)的函数叫做正比例函数;正比例函数y=kx(k是常数,k≠0),当k>0时,直线y=kx依次经过第三、一象限,从左向右上升,y随x的增大而增大;当k<0时,直线y=kx依次经过第二、四象限,从左向右下降,y随x的增大而减小.

练习册系列答案
相关题目
12. 如图所示的几何体的主视图正确的是( )
如图所示的几何体的主视图正确的是( )
 如图所示的几何体的主视图正确的是( )
如图所示的几何体的主视图正确的是( )| A. |  | B. |  | C. |  | D. |  |
15.下列叙述正确的是( )
①三角形的中线、角平分线都是射线
②三角形的三条高线交于一点
③三角形的中线就是经过一边中点的线段
④三角形的三条角平分线交于一点
⑤三角形的中线将三角形分成面积相等的两个小三角形.
①三角形的中线、角平分线都是射线
②三角形的三条高线交于一点
③三角形的中线就是经过一边中点的线段
④三角形的三条角平分线交于一点
⑤三角形的中线将三角形分成面积相等的两个小三角形.
| A. | ④⑤ | B. | ①②④ | C. | ②④ | D. | ④ |
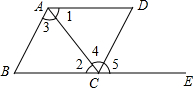 如图,下列能判定AB∥CD的条件有( )个.
如图,下列能判定AB∥CD的条件有( )个. 已知:如图,AB为半圆的直径,O为圆心,AD平分∠BAC交弦BC于F,DE⊥AC,垂足为E.
已知:如图,AB为半圆的直径,O为圆心,AD平分∠BAC交弦BC于F,DE⊥AC,垂足为E. 如图,在△ABC中,AB=AC,以AC为直径作⊙O交BC于D,P是AB延长线上一点,连PC,且∠PCB=$\frac{1}{2}$∠BAC
如图,在△ABC中,AB=AC,以AC为直径作⊙O交BC于D,P是AB延长线上一点,连PC,且∠PCB=$\frac{1}{2}$∠BAC