题目内容
6.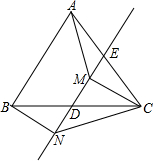 如图,△ABC是等边三角形,D是边BC的中点,过D的直线(不与直线BC重合)与边AC交于一点E,过顶点B,C分别作直线DE的垂线BN,CM垂足分别为N,M,连结AM,CN.
如图,△ABC是等边三角形,D是边BC的中点,过D的直线(不与直线BC重合)与边AC交于一点E,过顶点B,C分别作直线DE的垂线BN,CM垂足分别为N,M,连结AM,CN.(1)求证:BN=CM;
(2)当AM=CN时,求∠EDC的度数.
分析 (1)欲证明BN=CM,只要证明△BDN≌△CDM即可.
(2)由△AMC≌△CNB,推出△CDE是等边三角形即可解决问题.
解答 (1)证明: ∵BN⊥DE,CM⊥DE,
∵BN⊥DE,CM⊥DE,
∴∠BND=∠CMD=90°,
∵D是BC中点,
∴BD=CD,
在△BDN和△CDM中,
$\left\{\begin{array}{l}{∠BND=∠CMD}\\{∠BDN=∠CDM}\\{BD=CD}\end{array}\right.$,
∴△BDN≌△CDM,
∴BN=CM.
(2)∵△ABC是等边三角形,
∴AC=BC,∠ACB=60°,
在△AMC和△CNB中,
$\left\{\begin{array}{l}{AC=BC}\\{AM=CN}\\{CM=BN}\end{array}\right.$,
∴△AMC≌△CNB,
∴∠ACM=∠CBN,
∵∴△BDN≌△CDM,
∴∠CBN=∠MCD,
∴∠MCE=∠MCD=30°,
∵CM⊥DE,
∴∠CME=∠CMD=90°,
∴∠CEM=∠CDM=60°,
∴∠EDC=60°.
点评 本题考查等边三角形的性质、全等三角形的判定和性质等知识,解题的关键是正确寻找全等三角形解决问题,属于基础题,中考常考题型.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案
相关题目
16.宜昌市西陵区计划到2017年实现总收入4600亿元,这个数据用科学记数法表示为( )亿元.
| A. | 4.6×103 | B. | 4.6×104 | C. | 46×102 | D. | 0.46×104 |
17.下列各式符合代数式书写规范的是( )
| A. | a8 | B. | $\frac{s}{t}$ | C. | m-1元 | D. | 1$\frac{2}{5}$x |
1.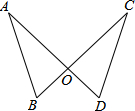 如图AB=CD,AD与BC交于点O,要使△AOB≌△COD,不添加辅助线则需条件是( )
如图AB=CD,AD与BC交于点O,要使△AOB≌△COD,不添加辅助线则需条件是( )
 如图AB=CD,AD与BC交于点O,要使△AOB≌△COD,不添加辅助线则需条件是( )
如图AB=CD,AD与BC交于点O,要使△AOB≌△COD,不添加辅助线则需条件是( )| A. | AO=CO | B. | BO=DO | C. | BC=AD | D. | ∠A=∠C |
16.当x=1时,下列分式的值为0的是( )
| A. | $\frac{x-1}{{{x^2}-1}}$ | B. | $\frac{x+1}{{{x^2}-1}}$ | C. | $\frac{1-x}{{{x^2}-1}}$ | D. | $\frac{{{x^2}-1}}{x+1}$ |
 如图,在△ABD和△AEC中,AD=AB,AC=AE,∠BAD=∠CAE.求证:DC=BE.
如图,在△ABD和△AEC中,AD=AB,AC=AE,∠BAD=∠CAE.求证:DC=BE. 如图,已知矩形ABCD,AB=1,又ABEF是正方形,若矩形CDEF与矩形ABCD相似,则AD长为:$\frac{\sqrt{5}+1}{2}$.
如图,已知矩形ABCD,AB=1,又ABEF是正方形,若矩形CDEF与矩形ABCD相似,则AD长为:$\frac{\sqrt{5}+1}{2}$. 如图,抛物线y=ax2-4x+c经过坐标原点O,且与x轴交于点A(-4,0)
如图,抛物线y=ax2-4x+c经过坐标原点O,且与x轴交于点A(-4,0)