ЬтФПФкШн
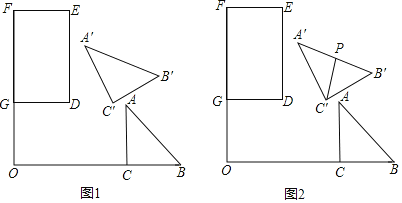
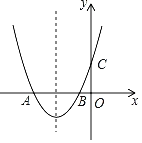
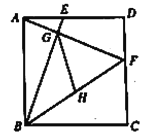
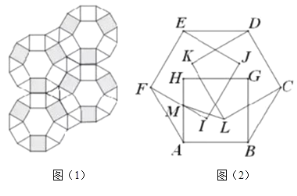
ЁОЬтФПЁПНЈжўЙЄШЫгУБпГЄЯрЕШЕФе§СљБпаЮЁЂе§ЗНаЮЁЂе§Ш§НЧаЮШ§жжДЩзЉЦЬЩшЕиУцЃЌе§ЗНаЮДЩзЉЗжКкАзСНжжбеЩЋЃЌУмЦЬГЩЭМЃЈ1ЃЉЕФаЮзДЃЎгУЫЎФрННжўЧАЃЌЮЊЗНБуЪЉЙЄЃЌЙЄШЫвЊЯШАбДЩзЉАДЭМ1ЗНЪНЯШАкЗХКУЃЌвЛЙЄШЫАкЗХЪБЃЌЮовтМфНЋ3ПщКкЩЋе§ЗНаЮДЩзЉЩЯЗЕНвЛИіе§СљБпаЮЕФЩЯУцЃЌЦфжаШ§Иіе§ЗНаЮЕФвЛЬѕБпЗжБ№КЭе§СљБпаЮЕФШ§ЬѕБпжиКЯЃЌШчЭМЃЈ2ЃЉЫљЪОЃЎАДЭМЃЈ2ЃЉЗНЪНИјИїЕузїЩЯБъзЂЃЌШєе§ЗНаЮЕФБпГЄ![]() ЃЌдђ
ЃЌдђ![]() _____
_____![]() (ВЛПМТЧДЩзЉЕФКёЖШ)
(ВЛПМТЧДЩзЉЕФКёЖШ)
ЁОД№АИЁП![]()
ЁОНтЮіЁП
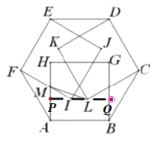
Й§ЕуIзї![]() ЃЌЗжБ№НЛAHгкЕуPЃЌНЛBGгкЕуQЃЌгЩе§СљБпаЮКЭе§ЗНаЮаджЪМЦЫу
ЃЌЗжБ№НЛAHгкЕуPЃЌНЛBGгкЕуQЃЌгЩе§СљБпаЮКЭе§ЗНаЮаджЪМЦЫу![]() ЕФЖШЪ§ЃЌдк
ЕФЖШЪ§ЃЌдк![]() жаЃЌБэЪОMPЃЌPIЃЌЕУLQЃЌPLЕФГЄЖШЃЌ
жаЃЌБэЪОMPЃЌPIЃЌЕУLQЃЌPLЕФГЄЖШЃЌ![]() жаЪЙгУЙДЙЩЖЈРэМЦЫуМДПЩЃЎ
жаЪЙгУЙДЙЩЖЈРэМЦЫуМДПЩЃЎ
Й§ЕуIзї![]() ЃЌЗжБ№НЛAHгкЕуPЃЌНЛBGгкЕуQ
ЃЌЗжБ№НЛAHгкЕуPЃЌНЛBGгкЕуQ
ИљОне§СљБпаЮЕФУПИіФкНЧЮЊЃК![]() ЃЌМД
ЃЌМД![]()
гжЁп![]() ЃЌЁр
ЃЌЁр![]()
ЭЌРэПЩЕУЃК![]()
Ёр![]() ЃЌ
ЃЌ![]()
Ёр![]() ЪЧЖЅНЧЮЊ120ЁуЕФЕШбќШ§НЧаЮ
ЪЧЖЅНЧЮЊ120ЁуЕФЕШбќШ§НЧаЮ
ЁпAF=AB=12
ЁрFM =AM=![]()
ЁрMI=![]()
дк![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]()
гЩе§СљБпаЮМАе§ЗНаЮаджЪПЩжЊЃК![]()
Ёр![]()
дк![]() жаЃЌ
жаЃЌ![]()
ЙЪД№АИЮЊЃК![]() ЃЎ
ЃЎ

СЗЯАВсЯЕСаД№АИ
 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИ
ЯрЙиЬтФП