题目内容
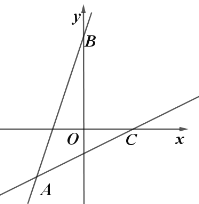
【题目】如图，在平面直角坐标系中，直线
交
轴于点
，现将直线绕点
顺时针方向旋转45°交
轴于点
，则直线
的函数表达式是_________．
【答案】
【解析】
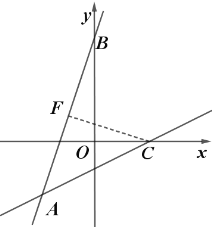
过点C作
交AB于点F，根据旋转
可得△FCA是等腰直角三角形，得到FC=AF，设C点的坐标为
，根据A，B的坐标可求出AB所在直线的解析式为
，根据直线垂直的特点可以求出FC所在的直线解析式为
，联立可得F的坐标为
，根据勾股定理可得出FC和AF的值，然后联立式子可求出C点的坐标，进而求的解析式．
过点C作交AB于点F．
设直线AB所在的直线解析式为
，由题可知
，
，得
设直线CF所在直线的解析式为
，
∵直线AB与直线CF垂直
∴
∴
∴
联立方程组得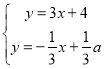
解得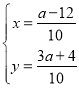
∴F ，根据题意可得
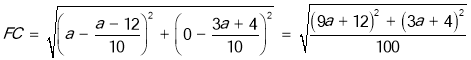
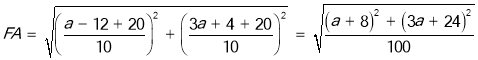
又∵
∴△FCA是等腰直角三角形 ∴FC=FA 得到 整理可得 得到 解方程可得: 所以得到C点的坐标为 设AC所在直线的解析式为 把A，C代入可得 ∴直线AC的函数表达式为 故答案为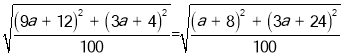
（舍去）
练习册系列答案
相关题目
