题目内容
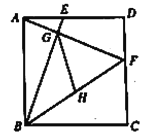
【题目】已知正方形![]() 的边长为6,点
的边长为6,点![]() ,
,![]() 分别在
分别在![]() ,
,![]() 上,
上,![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() ,点
,点![]() 为
为![]() 的中点,连接
的中点,连接![]() ,则
,则![]() 的长为______.
的长为______.
【答案】![]()
【解析】
根据正方形的四条边都相等可得AB=AD,每一个角都是直角可得∠BAE=∠D=90°,然后利用“边角边”证明△ABE≌△DAF得∠ABE=∠DAF,进一步得∠AGE=∠BGF=90°,从而知GH=![]() BF,利用勾股定理求出BF的长即可得出答案.
BF,利用勾股定理求出BF的长即可得出答案.
解:∵四边形ABCD为正方形,
∴∠BAE=∠D=90°,AB=AD,
在△ABE和△DAF中,
∵AB=AD,∠BAE=∠D, AE=DF,
∴△ABE≌△DAF(SAS),
∴∠ABE=∠DAF,
∵∠ABE+∠BEA=90°,
∴∠DAF+∠BEA=90°,
∴∠AGE=∠BGF=90°,
∵点H为BF的中点,
∴GH=![]() BF,
BF,
∵BC=6,CF=CDDF=62=4,
∴BF=![]() ,
,
∴GH=![]() ,
,
故答案为:![]() .
.

练习册系列答案
相关题目