题目内容
18.CO是△ACE的高,点B在OE上,OB=OA,AC=BE(1)如图1,求证:∠A=2∠E;
(2)如图2,CF是△ACE的角平分线.
①求证:AC+AF=CE;
②判断三条线段CE、EF、OF之间的数量关系,并给出证明.

分析 (1)连接CB,根据等腰三角形的性质和三角形的外角性质解答即可;
(2)①在CE上截取CH=CA,连接FH,利用全等三角形的判定和性质解答即可;
②根据全等三角形的性质进行解答即可.
解答 证明:(1)连接CB,由AO=OB,CO⊥AB,
∴CA=CB,
∴∠A=∠CBA,
∵AC=BE,
∴BE=CB,
∴∠E=∠BCE,
∴∠A=∠CBA=∠BCE+∠E=2∠E;
(2)①在CE上截取CH=CA,连接FH,
∵∠ACF=∠ECF,CF=CF,
在△FCA与△FCH中,
$\left\{\begin{array}{l}{CH=CA}\\{∠ACF=∠ECF}\\{CF=CF}\end{array}\right.$,
∴△FCA≌△FCH,
∴AF=HF,∠A=∠CHF=∠HFE+∠E=2∠E,
∴∠HFE=∠E,
∴AF=HE,
即CE=CH+HE=CA+AF;
②在①的基础上,BE=AC,AO=OB,
∴CE=CA+AF
=BE+AO+OF
=EF-FB+OB+OF
=EF+OF+OF
=EF+2OF.
点评 此题考查了全等三角形的判定与性质和等腰三角形的判定与性质以及等腰三角形的性质;证明三角形全等是解决问题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
8.Rt△ABC中,∠C=90°,AC=5,BC=12,则这个三角形外接圆的半径为( )
| A. | 2.5 | B. | 6 | C. | 6.5 | D. | 8.5 |
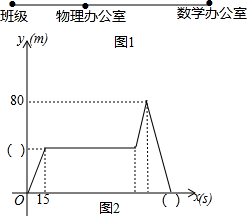 某校八(22)班同学上午第二节下课5分钟后,以2m/s的平均速度去物理老师办公室请教问题,他离班级距离y(m)与时间x(s)关系如图所示:
某校八(22)班同学上午第二节下课5分钟后,以2m/s的平均速度去物理老师办公室请教问题,他离班级距离y(m)与时间x(s)关系如图所示: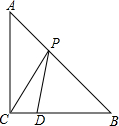 如图,在△ABC中,AC=BC=4,∠ACB=90°,D是BC边的一点,且CD=1,P是AB边上一动点,则PC+PD的最小值是5.
如图,在△ABC中,AC=BC=4,∠ACB=90°,D是BC边的一点,且CD=1,P是AB边上一动点,则PC+PD的最小值是5.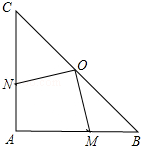 如图,在Rt△ABC中,∠A=90°,AB=AC=4cm,若O是BC的中点,动点M在AB移动,动点N在AC上移动,且AN=BM.
如图,在Rt△ABC中,∠A=90°,AB=AC=4cm,若O是BC的中点,动点M在AB移动,动点N在AC上移动,且AN=BM.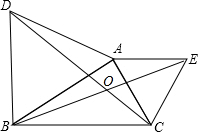 如图,△ABD和△AEC都是等边三角形;
如图,△ABD和△AEC都是等边三角形;