题目内容
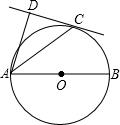如图，AB为⊙O的直径，C为⊙O上的一点，DA和过点C的切线互相垂直，垂足为D，若∠DAB=70°，求∠DAC的度数．考点：切线的性质
专题：
分析：连接OC，根据切线与圆的关系和直角三角形内角之间的关系，可以推出AC平分∠DAB，从而得出∠DAC的度数．
解答：
解：连接OC，
∵CD是切线，
∴OC⊥CD．
∵AD⊥CD，
∴AD∥CO，
∴∠1=∠3．
∵∠2=∠3，
∴∠1=∠2．
∵∠DAB=70°，
∴∠DAC=35°．
解：连接OC，∵CD是切线，
∴OC⊥CD．
∵AD⊥CD，
∴AD∥CO，
∴∠1=∠3．
∵∠2=∠3，
∴∠1=∠2．
∵∠DAB=70°，
∴∠DAC=35°．
点评：本题考查了切线的性质1，以及平行线的性质，在圆内的各边之间的关系．
练习册系列答案
相关题目
数轴上a、b两个实数的点的位置如图所示，化简|ab-b|-|a+ab|=
如图，C、D是直线l两侧的点，试在直线l上找一点Q，使|CQ-DQ|最大．
如图，PA切⊙O于点P，AB交⊙O于C，B两点，求证：∠APC=∠B．
如图，方格纸中的每个小方格都是边长为1个单位的正方形，在建立平面直角坐标系后，△ABC的顶点均在格点上，点C的坐标为（4，-1）．