题目内容
15. 如图,菱形OABC的顶点A的坐标为(2,0),∠COA=60°,将菱形OABC绕坐标原点O逆时针旋转120°得到菱形ODEF.
如图,菱形OABC的顶点A的坐标为(2,0),∠COA=60°,将菱形OABC绕坐标原点O逆时针旋转120°得到菱形ODEF.(1)直接写出点F的坐标;
(2)求线段OB的长及图中阴影部分的面积.
分析 (1)由菱形OABC的顶点A的坐标为(2,0),可求得OA=2,又由将菱形OABC绕坐标原点O逆时针旋转120°得到菱形ODEF,∠COA=60°,可得点F在x轴的负半轴上,且OF=2,继而求得点F的坐标;
(2)首先过点B作BG⊥x轴于点G,连接OE,OB,可求得∠AOB=∠EOF=30°,AB=OA=2,继而求得线段BG的长,则可求得扇形EOB与菱形OABC的面积,继而求得答案.
解答 解:(1)∵菱形OABC的顶点A的坐标为(2,0),
∴OA=2,
∵将菱形OABC绕坐标原点O逆时针旋转120°得到菱形ODEF,∠COA=60°,
∴∠AOF=180°,OF=2,
即点F在x轴的负半轴上,
∴点F(-2,0);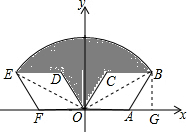 (2)过点B作BG⊥x轴于点G,连接OE,OB,
(2)过点B作BG⊥x轴于点G,连接OE,OB,
则∠AOB=∠EOF=30°,AB=OA=2,
∴∠BAG=60°,
∴∠ABG=30°,
∴AG=$\frac{1}{2}$AB=1,BG=$\sqrt{A{B}^{2}-A{G}^{2}}$=$\sqrt{3}$,
∴OB=2BG=2$\sqrt{3}$,
∵∠BOE=120°,
∴S扇形=$\frac{120×π×(2\sqrt{3})^{2}}{360}$=4π,S菱形OABC=OA•BG=2$\sqrt{3}$,
∴S阴影=S扇形-S菱形OABC=4π-2$\sqrt{3}$.
点评 此题考查了菱形的性质、旋转的性质以及扇形的面积.注意准确作出辅助线是解此题的关键.

练习册系列答案
相关题目
5.下列几何体的主视图与其他三个不同的是( )
| A. |  | B. |  | C. |  | D. |  |
6.甲、乙两布袋装有红、白两种小球,两袋装球总数量相同,两种小球仅颜色不同.甲袋中,红球个数是白球个数的2倍;乙袋中,红球个数是白球个数的3倍,将乙袋中的球全部倒入甲袋,随机从甲袋中摸出一个球,摸出红球的概率是( )
| A. | $\frac{5}{12}$ | B. | $\frac{7}{12}$ | C. | $\frac{17}{24}$ | D. | $\frac{2}{5}$ |
3. 如图,AB∥CD,点E在线段BC上,若∠1=40°,∠2=30°,则∠3的度数是( )
如图,AB∥CD,点E在线段BC上,若∠1=40°,∠2=30°,则∠3的度数是( )
 如图,AB∥CD,点E在线段BC上,若∠1=40°,∠2=30°,则∠3的度数是( )
如图,AB∥CD,点E在线段BC上,若∠1=40°,∠2=30°,则∠3的度数是( )| A. | 70° | B. | 60° | C. | 55° | D. | 50° |
10. 如图,四边形ABCD是⊙O的内接四边形,若∠A=70°,则∠C的度数是( )
如图,四边形ABCD是⊙O的内接四边形,若∠A=70°,则∠C的度数是( )
 如图,四边形ABCD是⊙O的内接四边形,若∠A=70°,则∠C的度数是( )
如图,四边形ABCD是⊙O的内接四边形,若∠A=70°,则∠C的度数是( )| A. | 100° | B. | 110° | C. | 120° | D. | 130° |
7.下列运算错误的是( )
| A. | $(\frac{1}{2})^{0}$=1 | B. | x2+x2=2x4 | C. | |a|=|-a| | D. | $(\frac{b}{{a}^{2}})^{3}$=$\frac{{b}^{3}}{{a}^{6}}$ |
4. 如图,已知∠ABC=∠DCB,下列所给条件不能证明△ABC≌△DCB的是( )
如图,已知∠ABC=∠DCB,下列所给条件不能证明△ABC≌△DCB的是( )
 如图,已知∠ABC=∠DCB,下列所给条件不能证明△ABC≌△DCB的是( )
如图,已知∠ABC=∠DCB,下列所给条件不能证明△ABC≌△DCB的是( )| A. | ∠A=∠D | B. | AB=DC | C. | ∠ACB=∠DBC | D. | AC=BD |
5.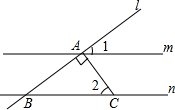 如图,m∥n,直线l分别交m,n于点A,点B,AC⊥AB,AC交直线n于点C,若∠1=35°,则∠2等于( )
如图,m∥n,直线l分别交m,n于点A,点B,AC⊥AB,AC交直线n于点C,若∠1=35°,则∠2等于( )
 如图,m∥n,直线l分别交m,n于点A,点B,AC⊥AB,AC交直线n于点C,若∠1=35°,则∠2等于( )
如图,m∥n,直线l分别交m,n于点A,点B,AC⊥AB,AC交直线n于点C,若∠1=35°,则∠2等于( )| A. | 35° | B. | 45° | C. | 55° | D. | 65° |