题目内容
11. 如图,CB=1,且OA=OB,BC⊥OC,则点A在数轴上表示的实数是( )
如图,CB=1,且OA=OB,BC⊥OC,则点A在数轴上表示的实数是( )| A. | $\sqrt{6}$ | B. | -$\sqrt{6}$ | C. | $\sqrt{5}$ | D. | -$\sqrt{5}$ |
分析 在RT△BCO中,利用勾股定理求出BO即可知道OA的长得出结论.
解答 解:∵BC⊥OC,
∴∠BCO=90°,
∵BC=1,CO=2,
∴OB=OA=$\sqrt{B{C}^{2}+O{C}^{2}}$=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$,
∵点A在原点左边,
∴点A表示的实数是-$\sqrt{5}$.
故选D.
点评 本题考查勾股定理、数轴上的点与实数之间的一一对应关系,求出OA的长度是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.将y=(x-2)2+3的图象向右平移2个单位,再向下平移2个单位,所得函数的对称轴和最小值分别为( )
| A. | x=4,y=1 | B. | x=2,y=3 | C. | x=4,y=3 | D. | x=0,y=5 |
6.下列各数中,不是无理数的是( )
| A. | $\sqrt{5}$ | B. | -3.14 | C. | $\root{3}{36}$ | D. | $\frac{π}{3}$ |
1. 如图是一个台阶示意图,每一层台阶的高都是20cm,宽都是50cm,长都是40cm,一只蚂蚁沿台阶从点A出发到点B,其爬行的最短线路的长度是( )
如图是一个台阶示意图,每一层台阶的高都是20cm,宽都是50cm,长都是40cm,一只蚂蚁沿台阶从点A出发到点B,其爬行的最短线路的长度是( )
 如图是一个台阶示意图,每一层台阶的高都是20cm,宽都是50cm,长都是40cm,一只蚂蚁沿台阶从点A出发到点B,其爬行的最短线路的长度是( )
如图是一个台阶示意图,每一层台阶的高都是20cm,宽都是50cm,长都是40cm,一只蚂蚁沿台阶从点A出发到点B,其爬行的最短线路的长度是( )| A. | 100cm | B. | 120cm | C. | 130cm | D. | 150cm |
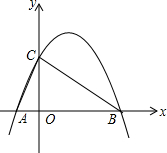 如图,已知抛物线y=-$\frac{1}{2}$x2+$\frac{3}{2}$x+2与x轴交于A、B两点(A左、右B),与y轴交于点C.
如图,已知抛物线y=-$\frac{1}{2}$x2+$\frac{3}{2}$x+2与x轴交于A、B两点(A左、右B),与y轴交于点C. 如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(-2,-1),B(-1,1),C(0,-2).
如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(-2,-1),B(-1,1),C(0,-2). 观察中国象棋的棋盘,其中“马”的位置可以用一个数对(3,5)来表示,则表示“兵”点位置的数对是(6,7).
观察中国象棋的棋盘,其中“马”的位置可以用一个数对(3,5)来表示,则表示“兵”点位置的数对是(6,7).