题目内容
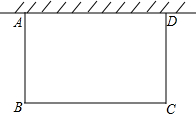 某居民小区要在一块一边靠墙(墙长15米)的空地上修建一个矩形花园ABCD,花园的一边靠墙,另三边用总长40米的栅栏围成(如图所示).若设花园的BC边长为x米,花园的面积为y平方米.
某居民小区要在一块一边靠墙(墙长15米)的空地上修建一个矩形花园ABCD,花园的一边靠墙,另三边用总长40米的栅栏围成(如图所示).若设花园的BC边长为x米,花园的面积为y平方米.(1)求y与x之间的函数关系式,并写出自变量x的取值范围;
(2)满足条件的花园面积能否达到150平方米?若能,请求出x的值;若不能,请说明理由;
(3)当x是多少时,矩形场地面积y最大?最大面积是多少?
考点:二次函数的应用,一元二次方程的应用
专题:
分析:(1)利用长方形的周长公式即可解答;
(2)利用长方形的面积列方程解答即可;
(3)设长方形的面积为S,利用面积计算方法列出二次函数,用配方法求最大值解答问题.
(2)利用长方形的面积列方程解答即可;
(3)设长方形的面积为S,利用面积计算方法列出二次函数,用配方法求最大值解答问题.
解答:解:(1)由题意可知BC为x米,
则AB=
=20-
,
∵矩形ABCD的面积=AB×BC,
∴y=(20-
)x=20x-
x2=-
x2+20x,
自变量x的取值范围为:0<x≤15;
(2)能达到,
由题意知,当y=150时,-
x2+20x=150,
解得:x1=10,x2=30(不合题意,舍去),
故x=10时,花园面积能达到150平方米;
(3)∵a=-
<0,
当0<x≤15时,y随x的增大而增大,
∴当x=15时,
y取最大值是-
×152+20×15=187.5,
答:当x是15米时,矩形场地面积y最大,最大面积是187.5平方米.
则AB=
| 40-x |
| 2 |
| x |
| 2 |
∵矩形ABCD的面积=AB×BC,
∴y=(20-
| x |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
自变量x的取值范围为:0<x≤15;
(2)能达到,
由题意知,当y=150时,-
| 1 |
| 2 |
解得:x1=10,x2=30(不合题意,舍去),
故x=10时,花园面积能达到150平方米;
(3)∵a=-
| 1 |
| 2 |
当0<x≤15时,y随x的增大而增大,
∴当x=15时,
y取最大值是-
| 1 |
| 2 |
答:当x是15米时,矩形场地面积y最大,最大面积是187.5平方米.
点评:此题主要考查了一元二次方程的应用以及二次函数的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程,再求解.注意利用墙长15m判定是否符合题意.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
2012年全国参加普通高等学校招生考试的人数约为9150000人,其中9150000用科学记数法表示为( )
| A、9.15×104 |
| B、9.15×105 |
| C、9.15×106 |
| D、9.15×107 |