题目内容
已知抛物线C:y=x2+2x-3.
(1)补全表中A,B两点的坐标,并在所给的平面直角坐标系中画出抛物线C;
(2)将抛物线C上每一点的横坐标变为原来的2倍,纵坐标变为原来的
,可证明得到的曲线仍是抛物线,(记为C1),且抛物线C1的顶点是抛物线C的顶点的对应点,求抛物线C1对应的函数表达式.
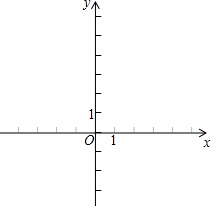
| 抛物线 | 顶点坐标 | 与x轴交点坐标 | 与y轴交点坐标 | |
| 抛物线C:y=x2+2x-3 | A( | B( | (1,0) | (0,-3) |
| 变换后的抛物线C1 | ||||
(2)将抛物线C上每一点的横坐标变为原来的2倍,纵坐标变为原来的
| 1 |
| 2 |
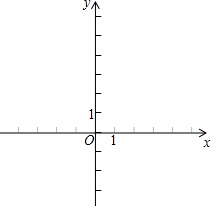
考点:抛物线与x轴的交点,二次函数图象与几何变换
专题:
分析:(1)利用配方法得到y=(x+1)2-4,根据二次函数的性质即可得到A点坐标,再令y=0得x2+2x-3=0,然后解方程即可得到B点坐标;再利用描点法画抛物线;
(2)利用抛物线C上每一点的横坐标变为原来的2倍,纵坐标变为原来的
,得到点A的对应点A1(-2,-2),点B的对应点B1(-6,0),由于抛物线C1的顶点坐标为A1(-2,-2),然后设顶点式求出抛物线C1的解析式.
(2)利用抛物线C上每一点的横坐标变为原来的2倍,纵坐标变为原来的
| 1 |
| 2 |
解答:解:(1)y=x2+2x-3=(x+1)2-4,则顶点A的坐标为(-1,-4),
当y=0时,x2+2x-3=0,解得x1=-3,x2=1,则B点坐标为(-3,0),(1,0),
如图;
(2)点A的对应点A1(-2,-2),点B的对应点B1(-6,0),
由于抛物线C1的顶点是抛物线C的顶点的对应点,
所以抛物线C1的顶点坐标为A1(-2,-2),
设抛物线C1的解析式为y=a(x+2)2-2,
把点B1(-6,0)代入得a•(-6+2)2-2=0,解得a=
,
所以抛物线C1的解析式为y=
(x+2)2-2=
x2+
x-
.
故答案为(-1,-4),(-3,0);A1(-2,-2),B1(-6,0),(2,0),(0,-
).

当y=0时,x2+2x-3=0,解得x1=-3,x2=1,则B点坐标为(-3,0),(1,0),
如图;
(2)点A的对应点A1(-2,-2),点B的对应点B1(-6,0),
由于抛物线C1的顶点是抛物线C的顶点的对应点,
所以抛物线C1的顶点坐标为A1(-2,-2),
设抛物线C1的解析式为y=a(x+2)2-2,
把点B1(-6,0)代入得a•(-6+2)2-2=0,解得a=
| 1 |
| 8 |
所以抛物线C1的解析式为y=
| 1 |
| 8 |
| 1 |
| 8 |
| 1 |
| 2 |
| 3 |
| 2 |
故答案为(-1,-4),(-3,0);A1(-2,-2),B1(-6,0),(2,0),(0,-
| 3 |
| 2 |
点评:本题考查了抛物线与x轴的交点:对于二次函数y=ax2+bx+c(a,b,c是常数,a≠0),△=b2-4ac决定抛物线与x轴的交点个数:当△=b2-4ac>0时,抛物线与x轴有2个交点;当△=b2-4ac=0时,抛物线与x轴有1个交点;当△=b2-4ac<0时,抛物线与x轴没有交点.

练习册系列答案
相关题目
| 1 |
| 6 |
| A、6 | ||
| B、-6 | ||
C、
| ||
D、-
|
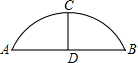 如图,某公园的一座石拱桥是圆弧形(劣弧),其跨度为24m,拱高为8m,则拱的半径为( )
如图,某公园的一座石拱桥是圆弧形(劣弧),其跨度为24m,拱高为8m,则拱的半径为( )| A、12m | B、8m |
| C、14m | D、13m |
 如图,已知在△ABC中,AD是边BC上的中线,设
如图,已知在△ABC中,AD是边BC上的中线,设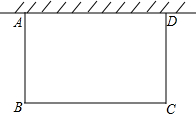 某居民小区要在一块一边靠墙(墙长15米)的空地上修建一个矩形花园ABCD,花园的一边靠墙,另三边用总长40米的栅栏围成(如图所示).若设花园的BC边长为x米,花园的面积为y平方米.
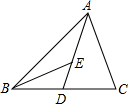
某居民小区要在一块一边靠墙(墙长15米)的空地上修建一个矩形花园ABCD,花园的一边靠墙,另三边用总长40米的栅栏围成(如图所示).若设花园的BC边长为x米,花园的面积为y平方米. 如图,已知D,E分别是△ABC的边BC和AC上的点,AE=2,CE=3,要使DE∥AB,那么BC:CD应等于
如图,已知D,E分别是△ABC的边BC和AC上的点,AE=2,CE=3,要使DE∥AB,那么BC:CD应等于