题目内容
19. 如图,Rt△ABC中,∠C=90°,AC=BC=6cm,E是斜边AB上任意一点,点E到两直角边的距离之和为6cm.
如图,Rt△ABC中,∠C=90°,AC=BC=6cm,E是斜边AB上任意一点,点E到两直角边的距离之和为6cm.
分析 推出四边形FCGE是矩形,得出FC=EG,FE=CG,EF∥CG,EG∥CA,求出∠BEG=∠B,推出EG=BG,同理AF=EF,求出EF+EG=AC=BC即可.
解答 解:∵∠C=90°,EF⊥AC,EG⊥BC,
∴∠C=∠EFC=∠EGC=90°,
∴四边形FCGE是矩形,
∴FC=EG,FE=CG,EF∥CG,EG∥CA,
∴∠BEG=∠A=45°=∠B,
∴EG=BG,
同理AF=EF,
∴EF+EG=CG+CB=BC=6cm,
故答案为:6.
点评 本题考查了等腰三角形的性质、等腰直角三角形、矩形的判定和性质,能求出矩形CFEG的周长=AC+BC是解此题的关键.

练习册系列答案
相关题目
7.如图,图1、图2、图3分别表示甲、乙、丙三人由A地到B地的路线图(箭头表示行进的方向),其中E为AB的中点,AH>HB,三人行进路线长度分别为l甲,l乙,l丙,则其大小关系正确的是( )


| A. | l甲<l乙<l丙 | B. | l乙<l丙<l甲 | C. | l丙<l乙<l甲 | D. | l甲=l乙=l丙 |
8.一个等腰三角形的顶角等于40°,则这个等腰三角形的底角度数是( )
| A. | 40° | B. | 50° | C. | 60° | D. | 70° |
9.已知:⊙O1、⊙O2的半径分别为3和6,且圆心距O1O2=3,则这两圆的位置关系是( )
| A. | 内切 | B. | 外切 | C. | 相交 | D. | 内含 |

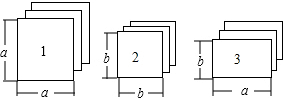

 如图的几何体,是由一个圆柱体从正中央挖去了一个与它等高的长方体后形成的,其俯视图如下,这个几何体的主视图是( )
如图的几何体,是由一个圆柱体从正中央挖去了一个与它等高的长方体后形成的,其俯视图如下,这个几何体的主视图是( )



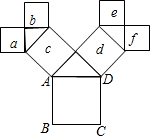 如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形ABCD的边长为6,则正方形a,b,c,d,e,f的面积和为72.
如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形ABCD的边长为6,则正方形a,b,c,d,e,f的面积和为72.