题目内容
如图所示，∠ACB=90°，CD⊥AB，垂足为D，则∠A+∠B=________，∠A=∠________，∠B=∠________．
90° 2 1
分析：根据三角形内角和定理得出∠A+∠B=90°即可，根据直角三角形性质得出∠A+∠1=90°，∠B+∠2=90°，即可求出答案
解答：∵∠ACB=90°，
∴∠A+∠B=180°-90°=90°，
∵CD⊥AB，
∴∠ADC=μBDC=90°，
∴∠A+∠1=90°，∠B+∠2=90°，
∴∠A=∠2，∠B=∠1，
故答案为：90°，2，1．
点评：本题考查了三角形内角和定理的应用，注意：三角形的内角和等于180°，直角三角形的两锐角互余．
分析：根据三角形内角和定理得出∠A+∠B=90°即可，根据直角三角形性质得出∠A+∠1=90°，∠B+∠2=90°，即可求出答案
解答：∵∠ACB=90°，
∴∠A+∠B=180°-90°=90°，
∵CD⊥AB，
∴∠ADC=μBDC=90°，
∴∠A+∠1=90°，∠B+∠2=90°，
∴∠A=∠2，∠B=∠1，
故答案为：90°，2，1．
点评：本题考查了三角形内角和定理的应用，注意：三角形的内角和等于180°，直角三角形的两锐角互余．
练习册系列答案
阅读快车系列答案
相关题目
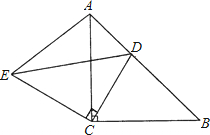如图所示，△ACB和△ECD都是等腰直角三角形，∠ACB=∠ECD=90°，D为AB边上一点．
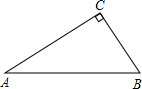才能使造价最低，请你画出水渠路线，并求出最低造价．
如图所示，∠ACB=90°，DE⊥AB，垂足为点E，AB=10，BC=6，求∠BDE的三个三角函数值．
如图所示，△ACB与△ECD都是等腰直角三角形，∠ACB=∠ECD=90°，点D为AB边上的一点，若AD=5，BD=12，求DE的长度，并说明理由．
如图所示，△ACB与△ECD都是等腰直角三角形，∠ACB=∠ECD=90°，点D为AB边上的一点，若AB=17，BD=12，