题目内容
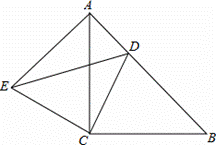
 如图所示,△ACB与△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,点D为AB边上的一点,若AD=5,BD=12,求DE的长度,并说明理由.
如图所示,△ACB与△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,点D为AB边上的一点,若AD=5,BD=12,求DE的长度,并说明理由.分析:由于△ACB与△ECD都是等腰直角三角形,CD=CE,CB=CA,∠B=∠CAB=45°,∠ACB=∠ECD=90°,于是∠ACE+∠ACD=∠ACD+∠BCD,根据等式性质可得∠ACE=∠BCD,利用SAS可证△ACE≌△BCD,于是∠EAC=∠B=45°,AE=BD=12,易求∠EAD=90°,再利用勾股定理可求DE=13.
解答:解:DE=13.
∵△ACB与△ECD都是等腰直角三角形,
∴CD=CE,CB=CA,∠B=∠CAB=45°,
∠ACB=∠ECD=90°,
即∠ACE+∠ACD=∠ACD+∠BCD,
∴∠ACE=∠BCD,
在△ACE和△BCD中,
∵
,
∴△ACE≌△BCD,
∴∠EAC=∠B=45°,AE=BD=12,
∴∠EAD=∠EAC+∠B=90°,
在Rt△EAD中,DE2=AE2+AD2=52+122=169,
∴DE=13.
故答案是13.

∵△ACB与△ECD都是等腰直角三角形,
∴CD=CE,CB=CA,∠B=∠CAB=45°,
∠ACB=∠ECD=90°,
即∠ACE+∠ACD=∠ACD+∠BCD,
∴∠ACE=∠BCD,
在△ACE和△BCD中,
∵
|
∴△ACE≌△BCD,
∴∠EAC=∠B=45°,AE=BD=12,
∴∠EAD=∠EAC+∠B=90°,
在Rt△EAD中,DE2=AE2+AD2=52+122=169,
∴DE=13.
故答案是13.
点评:本题考查了全等三角形的判定和性质、勾股定理,解题的关键是先证明△ACE≌△BCD,从而求出AE,以及∠EAD=90°.

练习册系列答案
相关题目
 如图所示,△ACB与△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,点D为AB边上的一点,若AB=17,BD=12,
如图所示,△ACB与△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,点D为AB边上的一点,若AB=17,BD=12,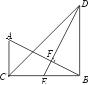
 如图所示,△ACB与△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,点D为AB边上的一点,若AD=5,BD=12,求DE的长度,并说明理由.
如图所示,△ACB与△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,点D为AB边上的一点,若AD=5,BD=12,求DE的长度,并说明理由.