题目内容
如图所示，∠ACB=90°，DE⊥AB，垂足为点E，AB=10，BC=6，求∠BDE的三个三角函数值．
分析：∵∠C=∠BED=90°，∠B=∠B，∴△ACB∽△DEB，则∠BDE=∠A，就可以转化为求∠A的三角函数值．
解答：解：∵△ACB∽△DEB，
∴∠BDE=∠A，
∴sin∠BDE=sinA=
，
cos∠BDE=cosA=
，
tan∠BDE=tanA=
．
∴∠BDE=∠A，
∴sin∠BDE=sinA=
| 3 |
| 5 |
cos∠BDE=cosA=
| 4 |
| 5 |
tan∠BDE=tanA=
| 3 |
| 4 |
点评：在两个三角形中有两个对应角相等，则这两三角形相似．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
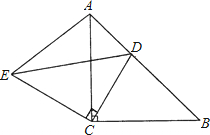如图所示，△ACB和△ECD都是等腰直角三角形，∠ACB=∠ECD=90°，D为AB边上一点．
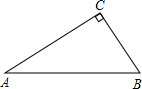才能使造价最低，请你画出水渠路线，并求出最低造价．
如图所示，△ACB与△ECD都是等腰直角三角形，∠ACB=∠ECD=90°，点D为AB边上的一点，若AD=5，BD=12，求DE的长度，并说明理由．
如图所示，△ACB与△ECD都是等腰直角三角形，∠ACB=∠ECD=90°，点D为AB边上的一点，若AB=17，BD=12，