题目内容
5．在平面直角坐标系中．对于平面内任一点（m，n），规定以下两种变换：①f（m，n）=（m，-n），如f（2，1）=（2，-1）；
②g（m，n）=（-m，-n），如g（2，1）=（-2，-1）．
按照以上变换有：f[g（3，4）]=f（-3，-4）=（-3，4），那么g[f（3，2）]等于（ ）
| A． | （3，2） | B． | （3．-2） | C． | （-3，2） | D． | （-3，-2） |
分析 根据f、g的规定进行计算即可得解．
解答 解：g[f（3，2）]=g（3，-2）=（-3，2）．
故选C．
点评 本题考查了点的坐标，读懂题目信息，理解f、g的运算方法是解题的关键．
练习册系列答案
阅读快车系列答案
相关题目
与
（a≠0）在同一直角坐标系中的图象可能是（ ）．
的值与
的值相等，则
的值为____．
(x＞0)图象上一点，连接OA，交函数y＝
(x＞0)的图象于点B，点C是x轴上一点，且AO＝AC，则△ABC的面积为________________.
10．
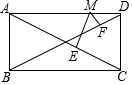如图，在矩形ABCD中，AB=5，AD=12，M是AD上异于A和D的任意一点，且ME⊥AC于E，MF⊥BD于F，则ME+MF为（ ）
如图，在矩形ABCD中，AB=5，AD=12，M是AD上异于A和D的任意一点，且ME⊥AC于E，MF⊥BD于F，则ME+MF为（ ）| A． | $\frac{60}{13}$ | B． | $\frac{30}{13}$ | C． | $\frac{15}{13}$ | D． | 不能确定 |
15．
如图，AD⊥BC于点D，GC⊥BC于点C，CF⊥AB于点F，下列关于高的说法中错误的是（ ）
如图，AD⊥BC于点D，GC⊥BC于点C，CF⊥AB于点F，下列关于高的说法中错误的是（ ）| A． | △AGC中，CF是AG边上的高 | B． | △GBC中，CF是BG边上的高 | ||
| C． | △ABC中，GC是BC边上的高 | D． | △GBC中，GC是BC边上的高 |
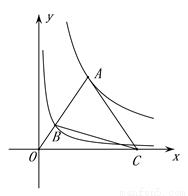
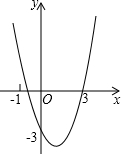如图，抛物线过（-1，0），（3，0），（0，-3）三点，沿x轴方向平移抛物线，使得以平移后的抛物线与x轴、y轴的三个交点为顶点的三角形面积为4，则符合条件的平移方式有（ ）
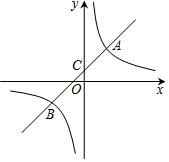如图，一次函数y=x+b的图象与反比例函数y=$\frac{k}{x}$的图象交于点A（3，6）与点B，且与y轴交于点C，若点P是反比例函数y=$\frac{k}{x}$图象上的一个动点，作直线AP与x轴、y轴分别交于点M、N，连结BN、CM．若S△ACM=S△ABN，则$\frac{AP}{AN}$的值为2或4．