题目内容
如图，已知在直角梯形ABCD中，AD∥BC，AB=BC，E为AB中点，BD⊥CE，BD，CE相交于M，连接AM交BC于G点．（1）求
| AM |
| MG |
（2）若S△ADM=S1，求S△CMG的面积．
考点：面积及等积变换,全等三角形的判定与性质,勾股定理,相似三角形的判定与性质
专题：综合题
分析：（1）易证△DAB≌△EBC，则有DA=EB．设DA=x，则BE=x，AB=BC=2x，根据勾股定理可得DB=
x．易证△EMB∽△DAB，根据相似三角形的性质可求得BM=
x，即可得到DM=
x，由AD∥BC可得△ADM∽△GBM，运用相似三角形的性质就可解决问题．
（2）由△ADM∽△GBM可求得
=
，从而得到GB=
，CG=
x，进而可得S△MCG=2S△GBM．由△ADM∽△GBM可得
=
，由S△ADM=S1可求得S△GBM=
S1，进而得到S△MCG=
S1．
| 5 |
2
| ||
| 5 |
3
| ||
| 5 |
（2）由△ADM∽△GBM可求得
| AD |
| GB |
| 3 |
| 2 |
| 2x |
| 3 |
| 4 |
| 3 |
| S△ADM |
| S△GBM |
| 9 |
| 4 |
| 4 |
| 9 |
| 8 |
| 9 |
解答：解：（1）∵四边形ABCD直角梯形，BD⊥CE，
∴∠DAB=∠ABC=∠EMB=∠CMB=90°，
∴∠MCB=90°-∠MBC=∠MBE．
在△DAB和△EBC中，
，
∴△DAB≌△EBC，
∴DA=EB．
设DA=x，则AE=BE=x，AB=BC=2x，
∴DB=
=
x．
∵∠MBE=∠ABD，∠EMB=DAB，
∴△EMB∽△DAB，
∴
=
，
∴
=
，
∴BM=
x，
∴DM=DB-BM=
x-
x=
x，
∴
=
．
∵AD∥BC，
∴△ADM∽△GBM，
∴
=
=
=
．
（2）∵
=
，AD=x，∴GB=
，
∴CG=BC-GB=2x-
=
x，
∴CG=2GB，
∴S△MCG=2S△GBM．
∵△ADM∽△GBM，
∴
=（
）2=
．
∵S△ADM=S1，∴S△GBM=
S1，
∴S△MCG=
S1．
∴∠DAB=∠ABC=∠EMB=∠CMB=90°，
∴∠MCB=90°-∠MBC=∠MBE．
在△DAB和△EBC中，
|
∴△DAB≌△EBC，
∴DA=EB．
设DA=x，则AE=BE=x，AB=BC=2x，
∴DB=
| DA2+AB2 |
| 5 |
∵∠MBE=∠ABD，∠EMB=DAB，
∴△EMB∽△DAB，
∴
| BM |
| BA |
| BE |
| BD |
∴
| BM |
| 2x |
| x | ||
|
∴BM=
2
| ||
| 5 |
∴DM=DB-BM=
| 5 |
2
| ||
| 5 |
3
| ||
| 5 |
∴
| DM |
| BM |
| 3 |
| 2 |
∵AD∥BC，
∴△ADM∽△GBM，
∴
| AM |
| MG |
| AD |
| GB |
| DM |
| BM |
| 3 |
| 2 |
（2）∵
| AD |
| GB |
| 3 |
| 2 |
| 2x |
| 3 |
∴CG=BC-GB=2x-
| 2x |
| 3 |
| 4 |
| 3 |
∴CG=2GB，
∴S△MCG=2S△GBM．
∵△ADM∽△GBM，
∴
| S△ADM |
| S△GBM |
| DM |
| BM |
| 9 |
| 4 |
∵S△ADM=S1，∴S△GBM=
| 4 |
| 9 |
∴S△MCG=
| 8 |
| 9 |
点评：本题考查了全等三角形的判定与性质、相似三角形的判定与性质、勾股定理等知识，证到DA=EB并运用相似三角形的性质是解决第（1）小题的关键，运用相似三角形的性质及面积法是解决第（2）小题的关键．
练习册系列答案
课堂练加测系列答案
轻松课堂单元测试AB卷系列答案
相关题目
已知m、n为常数，代数式2x4y+mx|5-n|y+xy化简之后为单项式，则mn的值共有（ ）
| A、1个 | B、2个 | C、3个 | D、4个 |
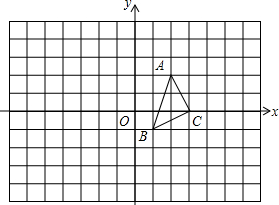已知平面直角坐标系中，△ABC的三个顶点的坐标分别为A（2，2），B（1，-1），C（3，0）．
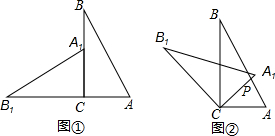将两块含30°角且大小相同的直角三角板如图①摆放，将图①中△A1B1C绕点C顺时针旋转45°得到图②，点P是A1C与AB的交点，若AP=2，AC的长为比x和y2的差的一半大5的数可表示为（ ）
A、
| ||
B、
| ||
| C、（x-y2）+5 | ||
| D、（x-y2）-5 |
若某件商品的原价为a元，提价10%后，欲恢复原价，应降价（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|