题目内容
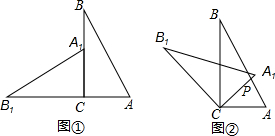 将两块含30°角且大小相同的直角三角板如图①摆放,将图①中△A1B1C绕点C顺时针旋转45°得到图②,点P是A1C与AB的交点,若AP=2,AC的长为
将两块含30°角且大小相同的直角三角板如图①摆放,将图①中△A1B1C绕点C顺时针旋转45°得到图②,点P是A1C与AB的交点,若AP=2,AC的长为考点:旋转的性质,勾股定理
专题:
分析:首先过点P作PD⊥AC于点D,由∠A=60°,AP=2,即可求得PD与AD的长,又由旋转的性质,可得△PCD是等腰直角三角形,即可求得答案.
解答: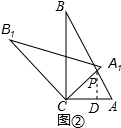 解:过点P作PD⊥AC于点D,
解:过点P作PD⊥AC于点D,
∵∠A=60°,AP=2,
∴AD=AP•cos60°=1,DP=AP•sin60°=
,
根据旋转的性质可得:∠A1CB=45°,
∵∠ACB=90°,
∴∠A1CA=45°,
∴△CDP是等腰直角三角形,
∴CD=PD=
,
∴AC=CD+AD=
+1.
故答案为:
+1.
 解:过点P作PD⊥AC于点D,
解:过点P作PD⊥AC于点D,∵∠A=60°,AP=2,
∴AD=AP•cos60°=1,DP=AP•sin60°=
| 3 |
根据旋转的性质可得:∠A1CB=45°,
∵∠ACB=90°,
∴∠A1CA=45°,
∴△CDP是等腰直角三角形,
∴CD=PD=
| 3 |
∴AC=CD+AD=
| 3 |
故答案为:
| 3 |
点评:此题考查了旋转的性质以及直角三角形的性质.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
一项工程,甲乙合作b天能完成,甲单独做需要a天完成,则乙单独完成这项工程需要( )天.
A、
| ||||
B、
| ||||
| C、a-b | ||||
D、
|
若-6xayzb与9x3ycz2是同类项,则a、b、c的值分别是( )
| A、a=3,b=2,c=1 |
| B、a=3,b=1,c=2 |
| C、a=1,b=2,c=3 |
| D、以上都不对 |
 如图,已知在直角梯形ABCD中,AD∥BC,AB=BC,E为AB中点,BD⊥CE,BD,CE相交于M,连接AM交BC于G点.
如图,已知在直角梯形ABCD中,AD∥BC,AB=BC,E为AB中点,BD⊥CE,BD,CE相交于M,连接AM交BC于G点.