题目内容
9.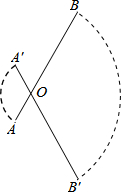 如图,点O是线段AB上一点,AB=4cm,AO=1cm,若线段AB绕点O顺时针旋转120°到线段A′B′的位置,则线段AB在旋转过程中扫过的图形的面积为( )
如图,点O是线段AB上一点,AB=4cm,AO=1cm,若线段AB绕点O顺时针旋转120°到线段A′B′的位置,则线段AB在旋转过程中扫过的图形的面积为( )| A. | 6πcm2 | B. | $\frac{10}{3}π$cm2 | C. | 9πcm2 | D. | 3πcm2 |
分析 将线段AB在旋转过程中扫过的图形看作两个扇形,运用扇形的面积公式求出两个扇形的面积,即可解决问题.
解答  解:如图,由题意得:OA=1,OB=3;
解:如图,由题意得:OA=1,OB=3;
∵${S}_{扇形A′OA}=\frac{120π•{1}^{2}}{360}$=$\frac{π}{3}$,${S}_{扇形BOB′}=\frac{120π•{3}^{2}}{360}$=3π,
∴线段AB在旋转过程中扫过的图形的面积=$\frac{π}{3}$+π=$\frac{10π}{3}$(cm2),
故选B.
点评 该题主要考查了扇形的面积公式及其应用问题;牢固掌握扇形的面积公式是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17. 如图,AB、CD相交于点O,AD∥CB,若AO=2,BO=3,CD=6,则CO等于( )
如图,AB、CD相交于点O,AD∥CB,若AO=2,BO=3,CD=6,则CO等于( )
 如图,AB、CD相交于点O,AD∥CB,若AO=2,BO=3,CD=6,则CO等于( )
如图,AB、CD相交于点O,AD∥CB,若AO=2,BO=3,CD=6,则CO等于( )| A. | 2.4 | B. | 3 | C. | 3.6 | D. | 4 |
4. 如图,点A、B分别在双曲线$y=\frac{1}{x}(x>0)$,$y=-\frac{4}{x}(x>0)$上,且OA⊥OB,则$\frac{OB}{OA}$的值为( )
如图,点A、B分别在双曲线$y=\frac{1}{x}(x>0)$,$y=-\frac{4}{x}(x>0)$上,且OA⊥OB,则$\frac{OB}{OA}$的值为( )
 如图,点A、B分别在双曲线$y=\frac{1}{x}(x>0)$,$y=-\frac{4}{x}(x>0)$上,且OA⊥OB,则$\frac{OB}{OA}$的值为( )
如图,点A、B分别在双曲线$y=\frac{1}{x}(x>0)$,$y=-\frac{4}{x}(x>0)$上,且OA⊥OB,则$\frac{OB}{OA}$的值为( )| A. | 1 | B. | $\sqrt{2}$ | C. | 2 | D. | $\sqrt{3}$ |
14.能使两个直角三角形全等的条件是( )
| A. | 斜边相等 | B. | 两直角边对应相等 | ||
| C. | 两锐角对应相等 | D. | 一锐角对应相等 |
18.下列多项式能分解因式的是( )
| A. | a2-b | B. | a2-4a+4 | C. | a2+ab+b2 | D. | a2+1 |
19. 如图,笑脸盖住的点的坐标可能是( )
如图,笑脸盖住的点的坐标可能是( )
 如图,笑脸盖住的点的坐标可能是( )
如图,笑脸盖住的点的坐标可能是( )| A. | (2,1) | B. | (-2,1) | C. | (-2,-1) | D. | (2,-1) |
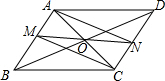 如图,?ABCD的对角线相交于点O,直线MN经过点O,分别写AB,CD交于点M,N,连接AN,CM.求证:四边形AMCN是平行四边形.
如图,?ABCD的对角线相交于点O,直线MN经过点O,分别写AB,CD交于点M,N,连接AN,CM.求证:四边形AMCN是平行四边形.