题目内容
19.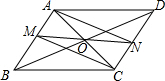 如图,?ABCD的对角线相交于点O,直线MN经过点O,分别写AB,CD交于点M,N,连接AN,CM.求证:四边形AMCN是平行四边形.
如图,?ABCD的对角线相交于点O,直线MN经过点O,分别写AB,CD交于点M,N,连接AN,CM.求证:四边形AMCN是平行四边形.
分析 先证明△OAM≌△CON,得出AM=CN,再根据平行四边形的判定方法即可得出结论.
解答 证明:∵四边形ABCD是平行四边形,
∴AB∥CD,OA=OC,
∴∠OAM=∠OCN,
在△OAM和△CON中,$\left\{\begin{array}{l}{∠OAM=∠OCN}&{\;}\\{OA=OC}&{\;}\\{∠AOM=∠CON}&{\;}\end{array}\right.$,
∴△OAM≌△CON(ASA),
∴AM=CN,
又∵AM∥CN,
∴四边形AMCN是平行四边形.
点评 本题考查了平行四边形的判定以及全等三角形的判定与性质;通过证明三角形全等得出对应边相等是解决问题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
14.下列事件中,属于必然事件的是( )
| A. | 二次函数的图象是抛物线 | |
| B. | 任意一个一元二次方程都有实数根 | |
| C. | 三角形的外心在三角形的外部 | |
| D. | 投掷一枚均匀的硬币100次,正面朝上的次数为50次 |
9.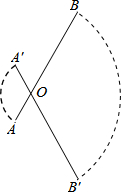 如图,点O是线段AB上一点,AB=4cm,AO=1cm,若线段AB绕点O顺时针旋转120°到线段A′B′的位置,则线段AB在旋转过程中扫过的图形的面积为( )
如图,点O是线段AB上一点,AB=4cm,AO=1cm,若线段AB绕点O顺时针旋转120°到线段A′B′的位置,则线段AB在旋转过程中扫过的图形的面积为( )
 如图,点O是线段AB上一点,AB=4cm,AO=1cm,若线段AB绕点O顺时针旋转120°到线段A′B′的位置,则线段AB在旋转过程中扫过的图形的面积为( )
如图,点O是线段AB上一点,AB=4cm,AO=1cm,若线段AB绕点O顺时针旋转120°到线段A′B′的位置,则线段AB在旋转过程中扫过的图形的面积为( )| A. | 6πcm2 | B. | $\frac{10}{3}π$cm2 | C. | 9πcm2 | D. | 3πcm2 |
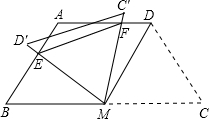 如图,等腰梯形ABCD中,AD∥BC,AD=AB=CD=2,∠C=60°,M是BC的中点.
如图,等腰梯形ABCD中,AD∥BC,AD=AB=CD=2,∠C=60°,M是BC的中点. 如图,直线a∥b,直线c与a,b相交,若∠2=70°,则∠1=110°.
如图,直线a∥b,直线c与a,b相交,若∠2=70°,则∠1=110°.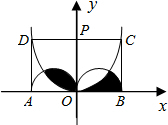 如图,矩形ABCD的长AB=4cm,点O是AB的中点,OP⊥AB,两半圆的直径分别为AO与OB.以AB、OP所在直线为两轴建立直角坐标系,抛物线y=ax2经过C、D两点,则图中阴影部分的面积是$\frac{π}{2}$cm2.
如图,矩形ABCD的长AB=4cm,点O是AB的中点,OP⊥AB,两半圆的直径分别为AO与OB.以AB、OP所在直线为两轴建立直角坐标系,抛物线y=ax2经过C、D两点,则图中阴影部分的面积是$\frac{π}{2}$cm2.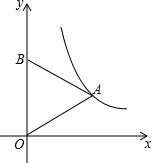 如图,等边三角形OAB的顶点A在反比例函数y=$\frac{\sqrt{3}}{x}$的图象上,点B在y轴上,若将△OAB沿x轴正方向平移,当点B落在反比例函数的图象上时,点A的坐标为($\frac{3\sqrt{3}}{2}$,1).
如图,等边三角形OAB的顶点A在反比例函数y=$\frac{\sqrt{3}}{x}$的图象上,点B在y轴上,若将△OAB沿x轴正方向平移,当点B落在反比例函数的图象上时,点A的坐标为($\frac{3\sqrt{3}}{2}$,1).