题目内容
已知梯形ABCD, AD∥BC,AB⊥BC,AD=1,AB=2,BC=3,问题:
(1)如图1,P为AB边上一点,以PD、PC为边做平行四边形PCQD,请问对角线PQ,DC的长能否相等,为什么?
(2)如图2,P为AB边上任意一点,以PD、PC为边做平行四边形PCQD,请问对角线PQ的长是否存在最小值?若果存在,请求出最小值;如果不存在,请说明理由。
(3)P为AB边上任意一点,延长PD到E,使DE=PD,以PE、PC为边做平行四边形PCQE,请探究对角线PQ的长是否也存在最小值?若果存在,请求出最小值;如果不存在,请说明理由。
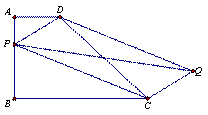
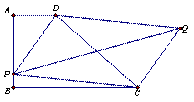
(图1) (图2)
(1)问题1:因为四边形PCQD是平行四边形,若对角线PQ、DC相等,则四边形PCQD是矩形。
所以∠DPC=90 ,因为AD=1,AB=2,BC=3.所以DC=2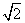 ,设PB=x,则AP=2-x,在Rt△DPC中,PD2+PC2=DC2,即x2+32+ (2-x)2+1=8,化简得x2-2x+3=0,
,设PB=x,则AP=2-x,在Rt△DPC中,PD2+PC2=DC2,即x2+32+ (2-x)2+1=8,化简得x2-2x+3=0,
因为△=(-2)2-4×1×3=-8<0,方程无解,所以对角线PQ与DC不可能相等
(2)问题2:如图1,在平行四边形PCQD中,设对角线PQ与DC相交于点G,所以点G是DC的中点,
作QH⊥BC,交BC的延长线于H。因为AD∥BC,所以∠ADC=∠DCH,即∠ADP+∠PDG=∠DCQ+QCH,
因为PD∥CQ,所以∠PDC=∠DCQ,所以∠ADP=∠QCH,,又PD=CQ,所以Rt△ADP≌Rt△HCQ,所以AD=HC……2分。因为AD=1,BC=3,所以BH=4,所以当PQ⊥AB时,PQ的长最小,即为4。
(3)问题3:如图2,设PQ与DC相较于点G。
因为PE∥CQ,PD=DE,所以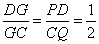 ,所以G是DC上一定点。作QH⊥BC,交BC的延长线于H,同理可证∠ADP=∠QCH,所以Rt△ADP∽Rt△HCQ 即
,所以G是DC上一定点。作QH⊥BC,交BC的延长线于H,同理可证∠ADP=∠QCH,所以Rt△ADP∽Rt△HCQ 即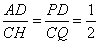 ,所以CH=2. 所以BH=BC+CH=3+2=5,,所以当PQ⊥AB时,PQ的长最小,即为5.
,所以CH=2. 所以BH=BC+CH=3+2=5,,所以当PQ⊥AB时,PQ的长最小,即为5.
(注:各题如有其它解法,只要正确,均可参照给分)
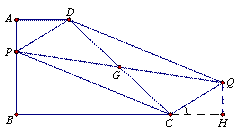
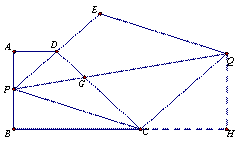
(图1) (图2)

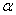 )为1︰1.2,坝高为5米。现为了提高堤坝的防洪抗洪能力,市防汛指挥部决定加固堤坝,要求坝顶CD加宽1米,形成新的背水坡EF,其坡度为1︰1.4。已知堤坝总长度为4000米。
)为1︰1.2,坝高为5米。现为了提高堤坝的防洪抗洪能力,市防汛指挥部决定加固堤坝,要求坝顶CD加宽1米,形成新的背水坡EF,其坡度为1︰1.4。已知堤坝总长度为4000米。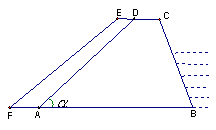
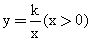 的图象交EF于点B,则点B的坐标为 .
的图象交EF于点B,则点B的坐标为 .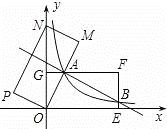
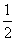 ;③梯形ABCD的面积为
;③梯形ABCD的面积为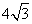 cm2;④点P从开始移动到停止移动一共用了(
cm2;④点P从开始移动到停止移动一共用了(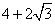 )秒;其中正确的结论是( )。
)秒;其中正确的结论是( )。 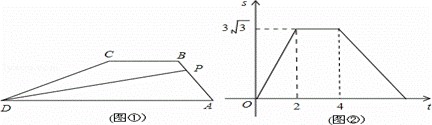
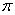 )。
)。
 的无理数:____ ___.
的无理数:____ ___. (改编)
(改编)