题目内容
如图，已知⊙O中，圆心角∠AOB=100°，则圆周角∠ACB等于
- A.130°
- B.120°
- C.110°
- D.100°
A
分析：在优弧AB上任取一点D，作圆周角∠ADB，根据圆周角定理易求得∠ADB的度数，由于四边形ADBC内接于⊙O，则∠D与∠C互补，由此得解．
解答：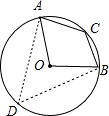
解：设点D是优弧AB上一点（不与A、B重合），连接AD、BD；
则∠ADB=
∠AOB=50°；
∵四边形ADBC内接于⊙O，
∴∠C=180°-∠ADB=130°；
故选A．
点评：此题主要考查的是圆周角定理及圆内接四边形的性质．
分析：在优弧AB上任取一点D，作圆周角∠ADB，根据圆周角定理易求得∠ADB的度数，由于四边形ADBC内接于⊙O，则∠D与∠C互补，由此得解．
解答：
解：设点D是优弧AB上一点（不与A、B重合），连接AD、BD；则∠ADB=
∠AOB=50°；∵四边形ADBC内接于⊙O，
∴∠C=180°-∠ADB=130°；
故选A．
点评：此题主要考查的是圆周角定理及圆内接四边形的性质．
练习册系列答案
相关题目
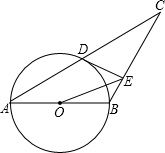OE，CD=
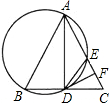如图，已知△ABC中，AB=AC，以AB为直径画圆，交BC于D，交AC于E，过D作DF⊥CE，垂足为F．由上述条件（不另增字母或添线），请你写出三个你认为是正确的结论（不要求证明）．
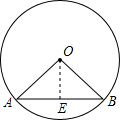如图，已知⊙O中，弦AB=12cm，O点到AB的距离等于AB的一半，则∠AOB的度数为
OA为半径的圆与边AB交于点D（点A除外），设OB=x，AD=y，
如图：已知⊙O中，AB=