题目内容
 如图:已知⊙O中,AB=4
如图:已知⊙O中,AB=4| 3 |
分析:先利用同弧所对的圆周角等于所对的圆心角的一半,求出扇形的圆心角为120度,直接根据圆锥的侧面展开图扇形的弧长等于圆锥底面周长可得圆锥的底面圆的半径,进而利用勾股定理得出即可.
解答: 解:过O作OE⊥AB于E,则
解:过O作OE⊥AB于E,则
AE=
AB=2
.
在Rt△AEO中,∠BAC=30°,cos30°=
.
∴OA=
=
=4.
又∵OA=OB,
∴∠ABO=30°.
∴∠BOC=60°.
∵AC⊥BD,
∴
=
.
∴∠COD=∠BOC=60°.
∴∠BOD=120°.
设圆锥的底面圆的半径为r,则周长为2πr,
∴2πr=
π×4.
∴r=
,
∴阴影部分所围成圆锥的高为:
=
.
 解:过O作OE⊥AB于E,则
解:过O作OE⊥AB于E,则AE=
| 1 |
| 2 |
| 3 |
在Rt△AEO中,∠BAC=30°,cos30°=
| AE |
| OA |
∴OA=
| AE |
| cos30° |
2
| ||||
|
又∵OA=OB,
∴∠ABO=30°.
∴∠BOC=60°.
∵AC⊥BD,
∴
 |
| BC |
 |
| CD |
∴∠COD=∠BOC=60°.
∴∠BOD=120°.
设圆锥的底面圆的半径为r,则周长为2πr,
∴2πr=
| 120 |
| 180 |
∴r=
| 4 |
| 3 |
∴阴影部分所围成圆锥的高为:
42-(
|
8
| ||
| 3 |
点评:本题主要考查了圆锥的侧面展开图与底面周长之间的关系和垂径定理等知识,求出圆的半径是解题关键.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
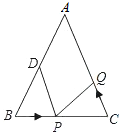 如图,已知△ABC中,AB=AC=10cm,BC=8cm,点D为AB的中点.
如图,已知△ABC中,AB=AC=10cm,BC=8cm,点D为AB的中点. 29、如图,已知△ABC中,AD⊥BC于D,AD=BD,DC=DE.求证:∠C=∠1.
29、如图,已知△ABC中,AD⊥BC于D,AD=BD,DC=DE.求证:∠C=∠1. 34、如图,已知△ABC中,AB=AC,AB的垂直平分线交AB于D,交AC于E,若△ABC与△EBC的周长分别是26cm、18cm,则AC=
34、如图,已知△ABC中,AB=AC,AB的垂直平分线交AB于D,交AC于E,若△ABC与△EBC的周长分别是26cm、18cm,则AC= 如图,已知△ABC中,AD=DB,D、E分别为BC、AB上一点,连接DE,∠1=∠2.
如图,已知△ABC中,AD=DB,D、E分别为BC、AB上一点,连接DE,∠1=∠2. 如图,已知△ABC中,AB>AC,BE、CF都是△ABC的高,P是BE上一点且BP=AC,Q是CF延长线上一点且CQ=AB,连接AP、AQ、QP,求证:
如图,已知△ABC中,AB>AC,BE、CF都是△ABC的高,P是BE上一点且BP=AC,Q是CF延长线上一点且CQ=AB,连接AP、AQ、QP,求证: