题目内容
2.已知A(-1,y1)、B(-2,y2)两点在双曲线y=$\frac{1-2m}{x}$上,且y1<y2,则m的取值范围是( )| A. | m>-$\frac{1}{2}$ | B. | m<-$\frac{1}{2}$ | C. | m>$\frac{1}{2}$ | D. | m<$\frac{1}{2}$ |
分析 将A(-1,y1),B(-2,y2)两点分别代入双曲线y=$\frac{1-2m}{x}$,求出 y1与y2的表达式,再根据 y1>y2则列不等式即可解答.
解答 解:将A(-1,y1),B(-2,y2)两点分别代入双曲线y=$\frac{1-2m}{x}$得,
y1=2m-1,
y2=m-$\frac{1}{2}$,
∵y1<y2,
∴2m-1<m-$\frac{1}{2}$,
解得m<$\frac{1}{2}$,
故选D.
点评 本题考查了反比例函数图象上点的坐标特征,要知道,反比例函数图象上的点符合函数解析式.

练习册系列答案
相关题目
12.下列计算正确的是( )
| A. | x3-x=x2 | B. | 3mn-4mn=-1 | C. | 5xy-y=5x | D. | -ab+3ba=2ab |
17.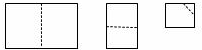 将一张矩形纸片对折,再对折,将所得矩形撕去一角,打开的图形一定有( )条对称轴.
将一张矩形纸片对折,再对折,将所得矩形撕去一角,打开的图形一定有( )条对称轴.
 将一张矩形纸片对折,再对折,将所得矩形撕去一角,打开的图形一定有( )条对称轴.
将一张矩形纸片对折,再对折,将所得矩形撕去一角,打开的图形一定有( )条对称轴.| A. | 一条 | B. | 二条 | C. | 三条 | D. | 四条 |
7.下列方程是一元二次方程的是( )
| A. | x2=0 | B. | $\frac{1}{{{x^2}+2x}}$=0 | C. | x3-2x2+x-1=0 | D. | x2+2xy+2=0 |
12.下列计算错误的是( )
| A. | $\sqrt{12}$÷$\sqrt{3}$=2 | B. | $\sqrt{8}=2\sqrt{2}$ | C. | $\sqrt{2}•\sqrt{3}$=$\sqrt{6}$ | D. | $\sqrt{2}+\sqrt{3}=\sqrt{5}$ |
 在数轴上表示出以下各数,并把这些数由小到大用“<”号连接起来.
在数轴上表示出以下各数,并把这些数由小到大用“<”号连接起来. 一次函数y=2x+2与反比例函数y=$\frac{k}{x}$(k≠0)的图象都经过点A(1,m),y=2x+2的图象与x轴交于点B.
一次函数y=2x+2与反比例函数y=$\frac{k}{x}$(k≠0)的图象都经过点A(1,m),y=2x+2的图象与x轴交于点B.