Question

【题目】如图，已知，，，且、、三点共线，与交于点．

（1）求证：；

（2）若，，则 ．

Answer 1

【答案】（1）见详解（2）2

【解析】

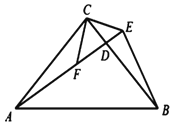
(1)如图1中，欲证明需先证明AF=BE，只要证明△ACF≌△BCE即可.
(2)如图1中，由△ACF≌△BCE，推出∠AFC=∠CEB,由∠CFE=∠CEF=45°，推出∠AFC=∠CEB=135°推出∠AEB=90°，由AC=BC=，推出BC=AC=,在Rt△AEB中，AE=推出EF=2，由此即可解决问题.

证明:如图中,∵∠ACB=∠FCE=90°∴∠ACF=∠BCE
在△ACF和BCE中,

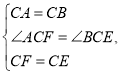
∴△ACF≌△BCE(SAS).

∴ AF=BE,

∴∠CAF=∠CBE,
∵∠CAE+∠EAB+∠ABC=90°
∴∠EAB+∠ABC+∠CBE=90°

∴∠AEB=90

在Rt△AEB中，
BE+AE=AB
∴AF+AE=AB,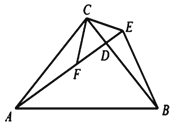

(2) ∵△ACF≌△BCE

∴∠AFC=∠CEB

∵，

∵∠CFE=∠CEF=45°

∴∠AFC=∠CEB=135°,

∴∠AEB=90°,
∵AC=BC=

∴BC=AC=,
∵BE=3 =AF
在Rt△AEB中，AE=
∴EF=2
故答案为:2