题目内容
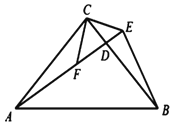
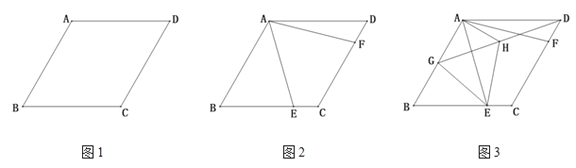
【题目】如图，在菱形ABCD中，∠ABC+∠ADC=120°，将一透明三角板60°角的顶点落在点A上，并绕着点A旋转，三角板的两边分别交BC、CD于点E、F．
（1）如图1，求∠BAD的度数；
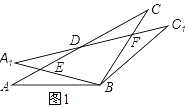
（2）如图2，求证：BE+DF=AB；
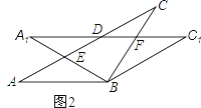
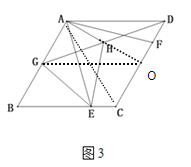
（3）如图3，在（2）的条件下，取AB中点G，作等边△EGH，连接AH，延长GH刚好与平行四边形ABCD交于点D，若AH⊥AB，△EGH的面积为
．求DH的长．
【答案】（1）120° （2）证明见解析 （3）
【解析】
（1）根据菱形和平行线的性质可得
，再根据
，可得
，即可求出
的度数；
（2）连接AC，根据菱形的性质和三角板的性质可得△ACD和△ABC是等边三角形，即可证明
，可得
，即可得证
；；
（3）延长AH与CD交于点O，连接AC、OG，通过证明四边形AGOD是平行四边形，可得
，再根据勾股定理求出GH的长度即可．
（1）∵四边形ABCD是菱形
∴
∵
∴
∴
；
（2）连接AC
根据三角板的性质得
∵四边形ABCD是菱形，
∴
∴△ACD和△ABC是等边三角形
∴
∴
在△ACE和△ADF中
∴
∴
∴
∴；
（3）延长AH与CD交于点O，连接AC、OG
∵
∴
∴
∴
∴
∵四边形ABCD是菱形
∴
∴△ACD是等边三角形
∴
∵G是AB的中点
∴
∴四边形AGOD是平行四边形
∴GH、HD是平行四边形AGOD的对角线
∴
∵△EGH是等边三角形，△EGH的面积为
∴
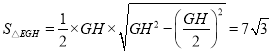
解得
∴
．
【题目】某校为了了解某个年级的学习情况，在这个年级抽取了50名学生，对某学科进行测试，将所得成绩(成绩均为整数)整理后，列出表格：
分组 | 50～59分 | 60～69分 | 70～79分 | 80～89分 | 90～99分 |
频率 | 0.04 | 0.04 | 0.16 | 0.34 | 0.42 |
(1)本次测试90分以上的人数有________人；(包括90分)
(2)本次测试这50名学生成绩的及格率是________；(60分以上为及格，包括60分)
(3)这个年级此学科的学习情况如何？请在下列三个选项中，选一个填在题后的横线上________．
A．好 B．一般 C．不好
