题目内容
11.小明写出如下一组数:$\frac{1}{5}$,-$\frac{3}{9}$,$\frac{7}{17}$,-$\frac{15}{33}$,…,请用你发现的规律,猜想第2014个数为-$\frac{{2}^{2014}-1}{{2}^{2015}+1}$.分析 首先判断出每个数的正负,然后根据每个数的分子分别是1、3、7、15、…,判断出第n个数的分子是多少;最后根据每个数的分母分别是5、9、17、33、…,判断出第n个数的分母是多少,进而判断出这组数的第n个数是多少,再把n=2014代入,求出第2014个数为多少即可.
解答 解:∵这组数分别是正数、负数、正数、负数、…,
∴这组数的第n个数的正负即(-1)n+1的正负;
∵1=21-1,3=22-1,7=23-1,15=24-1,
∴第n个数的分子是:2n-1;
∵5=4×(21-1-1)+5,9=4×(22-1-1)+5,17=4×(23-1-1)+5,33=4×(24-1-1)+5,
∴第n个数的分母是:4×(2n-1-1)+5=2n+1+1;
∴这组数的第n个数是:
(-1)n+1•$\frac{{2}^{n}-1}{{2}^{n+1}+1}$,
∴第2014个数为:
(-1)2014+1•$\frac{{2}^{2014}-1}{{2}^{2015}+1}$=-$\frac{{2}^{2014}-1}{{2}^{2015}+1}$.
故答案为:-$\frac{{2}^{2014}-1}{{2}^{2015}+1}$.
点评 此题主要考查了探寻数列规律问题,注意观察总结规律,并能正确的应用规律,解答此题的关键是求出这组数的第n个数是多少.

练习册系列答案
相关题目
2.设边长为a的正方形的面积为2.下列关于a的四种说法:
①a是2的算术平方根;②a是无理数;③a可以用数轴上的一个点来表示; ④0<a<1.
其中,所有正确说法的序号是( )
①a是2的算术平方根;②a是无理数;③a可以用数轴上的一个点来表示; ④0<a<1.
其中,所有正确说法的序号是( )
| A. | 12 | B. | 13 | C. | 123 | D. | 234 |
19.下列算式结果为-3的是( )
| A. | -|-3| | B. | (-3)0 | C. | -(-3) | D. | (-3)-1 |
16.某省各级各部门已筹集抗旱救灾救济资金32亿元,32亿元用科学记数法表示为( )
| A. | 3.2×108元 | B. | 0.32×1010元 | C. | 3.2×109元 | D. | 32×108元 |
20.某市民政部门举行“即开式福利彩票”销售活动,发行彩票10万张(每张彩票2元),在这些彩票中,设置如下奖项:如果花2元钱购买一张彩票,那么所得的奖金不多于100元的概率是$\frac{3}{1000}$.
| 奖金(元) | 10000 | 5000 | 1000 | 500 | 100 | 50 |
| 数量(个) | 1 | 4 | 20 | 40 | 100 | 200 |
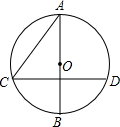 如图,半径为6的⊙O的直径AB与弦CD垂直,且∠BAC=40°,则劣弧BD的长是$\frac{8}{3}$π(结果保留π).
如图,半径为6的⊙O的直径AB与弦CD垂直,且∠BAC=40°,则劣弧BD的长是$\frac{8}{3}$π(结果保留π). 如图是汽车加油站在加油过程中,加油器仪表某一瞬间的显示,请你结合图片信息,解答下列问题:
如图是汽车加油站在加油过程中,加油器仪表某一瞬间的显示,请你结合图片信息,解答下列问题: