题目内容
1.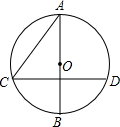 如图,半径为6的⊙O的直径AB与弦CD垂直,且∠BAC=40°,则劣弧BD的长是$\frac{8}{3}$π(结果保留π).
如图,半径为6的⊙O的直径AB与弦CD垂直,且∠BAC=40°,则劣弧BD的长是$\frac{8}{3}$π(结果保留π).
分析 连接OC、OD,由∠BAC=40°,根据圆周角定理求出∠BOC=2∠BAC=80°.再根据垂径定理得到$\widehat{BC}$=$\widehat{BD}$,利用圆心角、弧、弦的关系定理求出∠BOC=∠BOD=80°,然后根据弧长公式求解.
解答 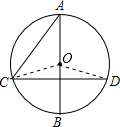 解:如图,连接OC、OD,
解:如图,连接OC、OD,
∵∠BAC=40°,
∴∠BOC=2∠BAC=80°.
∵⊙O的直径AB与弦CD垂直,
∴$\widehat{BC}$=$\widehat{BD}$,
∴∠BOC=∠BOD=80°,
∴劣弧BD的长是:$\frac{80π×6}{180}$=$\frac{8}{3}$π.
故答案为$\frac{8}{3}$π.
点评 本题考查了圆周角定理,垂径定理,圆心角、弧、弦的关系定理以及弧长的计算,求出∠BOD=80°是解题的关键.

练习册系列答案
相关题目
9.若a>b,则下列不等式中,错误的是( )
| A. | a-3>b-3 | B. | a+3>b+3 | C. | -3a>-3b | D. | $\frac{a}{3}$>$\frac{b}{3}$ |
6.下列“表情图”中,不属于轴对称图形的是( )
| A. | 流泪 | B. | 气晕 | C. | 不要啊 | D. | 苦瓜脸 |
10.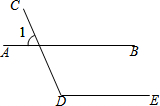 如图,∠1=50°,如果AB∥DE,那么∠D=( )
如图,∠1=50°,如果AB∥DE,那么∠D=( )
 如图,∠1=50°,如果AB∥DE,那么∠D=( )
如图,∠1=50°,如果AB∥DE,那么∠D=( )| A. | 40° | B. | 50° | C. | 130° | D. | 140° |
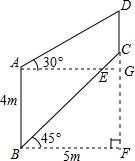 某大型机器零件的形状如图所示,已知AB∥DC,AE∥BF,根据图中数据,计算CD的长度(精确到十分位)
某大型机器零件的形状如图所示,已知AB∥DC,AE∥BF,根据图中数据,计算CD的长度(精确到十分位)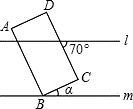 如图,l∥m,矩形ABCD的顶点B在直线m上,则∠α=20度.
如图,l∥m,矩形ABCD的顶点B在直线m上,则∠α=20度.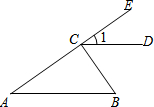 如图,∠ECB=92°,CD∥AB,∠B=57°,则∠1=35°.
如图,∠ECB=92°,CD∥AB,∠B=57°,则∠1=35°.