题目内容
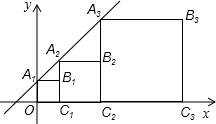 如图四边形A1B1C1O,A2B2C2C1,A3B3C3C2均为正方形.点A1,A2,A3和点C1,C2,C3分别在直线y=kx+b(k>0)和x轴上,点B3的坐标是(
如图四边形A1B1C1O,A2B2C2C1,A3B3C3C2均为正方形.点A1,A2,A3和点C1,C2,C3分别在直线y=kx+b(k>0)和x轴上,点B3的坐标是( ,
, ),则k+b=
),则k+b=
- A.1
- B.1.5
- C.2
- D.3.5
B
分析:首先设C1的坐标为(a,0),由四边形A1B1C1O,A2B2C2C1,A3B3C3C2均为正方形,点B3的坐标是( ,
, ),可求得A3的坐标是(
),可求得A3的坐标是( ,
, ),易证得△A2A1B1∽△A3A2B2,然后由相似三角形的对应边成比例,可求得a的值,又由点A1,A2,A3在直线y=kx+b(k>0)上,利用待定系数法即可求得k与b的值,继而求得答案.
),易证得△A2A1B1∽△A3A2B2,然后由相似三角形的对应边成比例,可求得a的值,又由点A1,A2,A3在直线y=kx+b(k>0)上,利用待定系数法即可求得k与b的值,继而求得答案.
解答:设C1的坐标为(a,0),
∵四边形A1B1C1O,A2B2C2C1,A3B3C3C2均为正方形,点B3的坐标是( ,
, ),
),
∴A3的坐标是:( -
- ,
, ),即(
),即( ,
, ),
),
∴A1B1=a,A2B2= -a,A2B1=
-a,A2B1= -a-a=
-a-a= -2a,A3B2=
-2a,A3B2= -(
-( -a)=a-
-a)=a- ,
,
∵A3在直线y=kx+b(k>0)上,
∴ k+b=
k+b= ①,
①,
∵A2C1∥A3C2,
∴∠A2A1B1=∠A3A2B2,
∵∠A2B1A1=∠A3B2A2=90°,
∴△A2A1B1∽△A3A2B2,
∴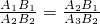 ,
,
∴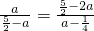 ,
,
整理得:4a2-29a+25=0,
解得:a= (舍去),a=1,
(舍去),a=1,
∴点A1(0,1),
∴b=1②,
把②代入①得:k=0.5,
∴k+b=1.5.
故选B.
点评:此题考查了正方形的性质、相似三角形的判定与性质以及待定系数法求一次函数解析式.此题难度较大,注意掌握数形结合思想与方程思想的应用.
分析:首先设C1的坐标为(a,0),由四边形A1B1C1O,A2B2C2C1,A3B3C3C2均为正方形,点B3的坐标是(
 ,
, ),可求得A3的坐标是(
),可求得A3的坐标是( ,
, ),易证得△A2A1B1∽△A3A2B2,然后由相似三角形的对应边成比例,可求得a的值,又由点A1,A2,A3在直线y=kx+b(k>0)上,利用待定系数法即可求得k与b的值,继而求得答案.
),易证得△A2A1B1∽△A3A2B2,然后由相似三角形的对应边成比例,可求得a的值,又由点A1,A2,A3在直线y=kx+b(k>0)上,利用待定系数法即可求得k与b的值,继而求得答案.解答:设C1的坐标为(a,0),
∵四边形A1B1C1O,A2B2C2C1,A3B3C3C2均为正方形,点B3的坐标是(
 ,
, ),
),∴A3的坐标是:(
 -
- ,
, ),即(
),即( ,
, ),
),∴A1B1=a,A2B2=
 -a,A2B1=
-a,A2B1= -a-a=
-a-a= -2a,A3B2=
-2a,A3B2= -(
-( -a)=a-
-a)=a- ,
,∵A3在直线y=kx+b(k>0)上,
∴
 k+b=
k+b= ①,
①,∵A2C1∥A3C2,
∴∠A2A1B1=∠A3A2B2,
∵∠A2B1A1=∠A3B2A2=90°,
∴△A2A1B1∽△A3A2B2,
∴
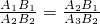 ,
,∴
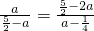 ,
,整理得:4a2-29a+25=0,
解得:a=
 (舍去),a=1,
(舍去),a=1,∴点A1(0,1),
∴b=1②,
把②代入①得:k=0.5,
∴k+b=1.5.
故选B.
点评:此题考查了正方形的性质、相似三角形的判定与性质以及待定系数法求一次函数解析式.此题难度较大,注意掌握数形结合思想与方程思想的应用.

练习册系列答案
相关题目
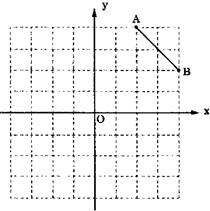
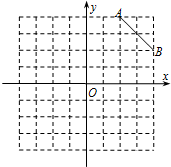 点C是第一象限内的一个格点,由点C与线段AB组成一个以AB为底,且腰长为无理数的等腰三角形.
点C是第一象限内的一个格点,由点C与线段AB组成一个以AB为底,且腰长为无理数的等腰三角形. 如图:是规格为8×8的正方形的网格,请你在所给的网格中按下列要求操作:
如图:是规格为8×8的正方形的网格,请你在所给的网格中按下列要求操作: