题目内容
在8×8的正方形网格中建立如图所示的平面直角坐标系,已知A(2,4),B(4,2).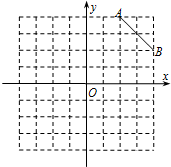 点C是第一象限内的一个格点,由点C与线段AB组成一个以AB为底,且腰长为无理数的等腰三角形.
点C是第一象限内的一个格点,由点C与线段AB组成一个以AB为底,且腰长为无理数的等腰三角形.(1)画出△ABC,点C的坐标是
(2)将△ABC绕点C旋转180°得到△A1B1C,连接AB1、BA1,试判断四边形AB1A1B是何种特殊四边形,请说明理由.
分析:(1)作线段AB的垂直平分线,第一象限内有3个格点,符合条件的只有一个(1,1),再用割补法求得面积即可;
(2)延长AC、BC至点A1、B1,使A1AC=AC,BC=BC1,即可得到△A1B1C,再根据矩形的判定定理:对角线平分且相等的四边形为矩形证得结论.
(2)延长AC、BC至点A1、B1,使A1AC=AC,BC=BC1,即可得到△A1B1C,再根据矩形的判定定理:对角线平分且相等的四边形为矩形证得结论.
解答:解:(1)如图,
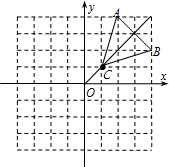
S△ABC=3×3-
×2×2-
×1×3-
×1×3
=9-2-1.5-1.5
=4;
(2)∵AC=BC,A1C=B1C,BC=B1C,AC=A1C,
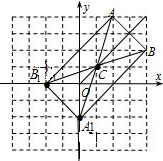
∴AA1=B1B,
∴四边形AB1A1B是矩形(对角线平分且相等的四边形为矩形).

S△ABC=3×3-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=9-2-1.5-1.5
=4;
(2)∵AC=BC,A1C=B1C,BC=B1C,AC=A1C,

∴AA1=B1B,
∴四边形AB1A1B是矩形(对角线平分且相等的四边形为矩形).
点评:本题考查了旋转的性质,坐标与图形的性质以及勾股定理,熟练掌握对角线平分且相等的四边形为矩形是矩形的重要判定定理.

练习册系列答案
相关题目
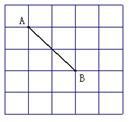
 (2011•岳池县模拟)在6×8的正方形网格中建立了如图所示的平面直角坐标系xoy,已知每个最小正方形边长为1,将图中的OA绕O点逆时针旋转90°得到OA′,则A′点坐标为
(2011•岳池县模拟)在6×8的正方形网格中建立了如图所示的平面直角坐标系xoy,已知每个最小正方形边长为1,将图中的OA绕O点逆时针旋转90°得到OA′,则A′点坐标为 如图,在10×10的正方形网格纸中(每个小方格的边长都是1个单位)有一个△ABC,请在网格纸中画出以点O为旋转中心把△ABC按顺时针方向旋转90°得到的△A′B′C′.
如图,在10×10的正方形网格纸中(每个小方格的边长都是1个单位)有一个△ABC,请在网格纸中画出以点O为旋转中心把△ABC按顺时针方向旋转90°得到的△A′B′C′.