题目内容
如图,在直线l上摆放有△ABC和直角梯形DEFG,且CD=6cm;在△ABC中:∠C=90°,∠A=30°,AB=4cm;在直角梯形DEFG中:EF∥DG,∠DGF=90°,DG=6cm,DE=4cm,∠EDG=60度.解答下列问题: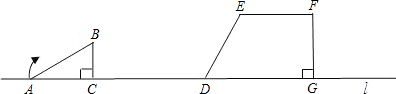
(1)旋转:将△ABC绕点C顺时针方向旋转90°,请你在图中作出旋转后的对应图形△A1B1C,并求出AB1的长度;
(2)翻折:将△A1B1C沿过点B1且与直线l垂直的直线翻折,得到翻折后的对应图形△A2B1C1,试判定四边形A2B1DE的形状并说明理由;
(3)平移:将△A2B1C1沿直线l向右平移至△A3B2C2,若设平移的距离为x,△A3B2C2与直角梯形重叠部分的面积为y,当y等于△ABC面积的一半时,x的值是多少.
分析:(1)根据旋转的定义得到CB′=CB,在直角三角形ABC中,根据三角函数就可以求出BC的长,即CB′的长,就可以求出AB1的长度;
(2)四边形A2B1DE是菱形,可以证明A2B与DE平行且相等,得到四边形A2B1DE是平行四边形,又A2B1=B1D=4,所以平行四边形A2B1DE是菱形.
(3)y等于△ABC面积的一半时有两种情况,一种是当A3B2与DE相交时,即当2≤x<4时:根据A3B2∥DE,得到则重合部分的三角形与△A3B2C2相似,且面积的比等于相似比,就可以求出在直线L上重合部分的长度,得到C1C2的长度.从而求出x的值.
另外一种情况是当A3B2与FG相交时,同样,根据三角形相似就可以求出C1C2的长度.从而求出x的值.
(2)四边形A2B1DE是菱形,可以证明A2B与DE平行且相等,得到四边形A2B1DE是平行四边形,又A2B1=B1D=4,所以平行四边形A2B1DE是菱形.
(3)y等于△ABC面积的一半时有两种情况,一种是当A3B2与DE相交时,即当2≤x<4时:根据A3B2∥DE,得到则重合部分的三角形与△A3B2C2相似,且面积的比等于相似比,就可以求出在直线L上重合部分的长度,得到C1C2的长度.从而求出x的值.
另外一种情况是当A3B2与FG相交时,同样,根据三角形相似就可以求出C1C2的长度.从而求出x的值.
解答: 解:(1)在△ABC中,由已知得:BC=2cm,AC=AB×cos30°=2
解:(1)在△ABC中,由已知得:BC=2cm,AC=AB×cos30°=2
cm,
∴AB1=AC+CB1=AC+CB=2+2
cm.
(2)四边形A2B1DE菱形.
理由如下:∵∠C=90°,∠A=30°,AB=4cm,
∴BC=
AB=
×4=2cm,
∵∠EDG=60°,∠A2B1C1=∠A1B1C=∠ABC=60°,
∴A2B1∥DE,
又∵A2B1=A1B1=AB=4cm,DE=4cm,
∴A2B1=DE,
∴四边形A2B1DE是平行四边形,
又∵A2B1=AB=4cm,
B1D=CD-B1C=6-2=4cm,
∴A2B1=B1D=4cm,
∴平行四边形A2B1DE是菱形.
(3)由题意可知:
S△ABC=
×2×2
=2
cm2,
①当0≤x<2或x≥10时,y=0,
此时重叠部分的面积不会等于△ABC的面积的一半.
②当2≤x<4时,直角边B2C2与直角梯形的下底边DG重叠的长度为DC2=C1C2-DC1=(x-2)cm,
则y=
(x-2)
(x-2)=
(x-2)2,
当y=
S△ABC=
时,即
(x-2)2=
解得x=2-
(舍)或x=2+
.
∴当x=2+
cm时,重叠部分的面积等于△ABC的面积的一半.
③当4cm≤x<8cm时,△A3B2C2完全与直角梯形重叠,即y=2
cm2.
④当8cm≤x<10cm时,B2G=B2C2-GC2=2-(x-8)=10-xcm
则y=
(10-x)•
(10-x)=
(10-x)2,
当y=
S△ABC=
时,即
(10-x)2=
,
解得x=10-
cm,或x=10+
cm(舍去).
∴当x=10-
cm时,重叠部分的面积等于△ABC的面积的一半.
由以上讨论知,当x=2+
cm或x=10-
cm时,重叠部分的面积等于△ABC的面积的一半.
 解:(1)在△ABC中,由已知得:BC=2cm,AC=AB×cos30°=2
解:(1)在△ABC中,由已知得:BC=2cm,AC=AB×cos30°=2| 3 |
∴AB1=AC+CB1=AC+CB=2+2
| 3 |
(2)四边形A2B1DE菱形.
理由如下:∵∠C=90°,∠A=30°,AB=4cm,
∴BC=
| 1 |
| 2 |
| 1 |
| 2 |
∵∠EDG=60°,∠A2B1C1=∠A1B1C=∠ABC=60°,
∴A2B1∥DE,
又∵A2B1=A1B1=AB=4cm,DE=4cm,
∴A2B1=DE,
∴四边形A2B1DE是平行四边形,
又∵A2B1=AB=4cm,
B1D=CD-B1C=6-2=4cm,
∴A2B1=B1D=4cm,
∴平行四边形A2B1DE是菱形.
(3)由题意可知:
S△ABC=
| 1 |
| 2 |
| 3 |
| 3 |
①当0≤x<2或x≥10时,y=0,
此时重叠部分的面积不会等于△ABC的面积的一半.
②当2≤x<4时,直角边B2C2与直角梯形的下底边DG重叠的长度为DC2=C1C2-DC1=(x-2)cm,
则y=
| 1 |
| 2 |
| 3 |
| ||
| 2 |
当y=
| 1 |
| 2 |
| 3 |
| ||
| 2 |
| 3 |
解得x=2-
| 2 |
| 2 |
∴当x=2+
| 2 |
③当4cm≤x<8cm时,△A3B2C2完全与直角梯形重叠,即y=2
| 3 |
④当8cm≤x<10cm时,B2G=B2C2-GC2=2-(x-8)=10-xcm
则y=
| 1 |
| 2 |
| 3 |
| ||
| 2 |
当y=
| 1 |
| 2 |
| 3 |
| ||
| 2 |
| 3 |
解得x=10-
| 2 |
| 2 |
∴当x=10-
| 2 |
由以上讨论知,当x=2+
| 2 |
| 2 |
点评:本题主要考查了旋转的性质,用运动变化的观点理解本题是解决的关键.

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
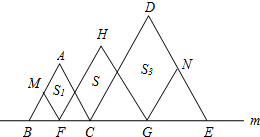 如图,在直线m上摆放着三个正三角形:△ABC、△HFG、△DCE,已知BC=
如图,在直线m上摆放着三个正三角形:△ABC、△HFG、△DCE,已知BC=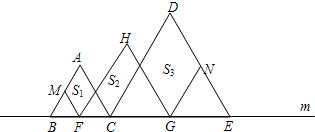 如图,在直线m上摆放着三个正三角形:△ABC、△HFG、△DCE,已知BC=GE,F、G分别是BC、CE的中点,FM∥AC,GN∥DC.设图中三个平行四边形的面积依次是S1,S2,S3,若S1+S3=20,则S2等于( )
如图,在直线m上摆放着三个正三角形:△ABC、△HFG、△DCE,已知BC=GE,F、G分别是BC、CE的中点,FM∥AC,GN∥DC.设图中三个平行四边形的面积依次是S1,S2,S3,若S1+S3=20,则S2等于( ) 若S1+S3=10,则S2=
若S1+S3=10,则S2=