题目内容
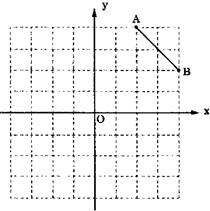
在8×8正方形网格中建立如图的平面直角坐标系，己知A（2，4），B（4，2）．
C是第一象限内一个格点，由点C与线段AB组成一个以AB为底，且腰长为无理数的等腰三角形.
1.填空：C点的坐标是_________，△ABC的面积是__________；
2.将△ABC绕点C旋转180°得到△A1B1C，连结AB1，BA1，试判断四边形AB1A1B是何种特殊四边形，请说明理由；
3.请探究：在x轴上是否存在这样的点P，使四边形ABOP的面积等于△ABC面积
2倍．若存在，请直接写出点P的坐标（不必写出解答过程）；若不存在，请说明理由．
【答案】
1. （1,1） ，4
2.四边形AB1A1B是矩形
3.（2,0），（-1,0）
【解析】（1）根据题意点C与线段AB组成一个以AB为底，且腰长为无理数的等腰三角形，
可知点C（1,1）.
（2）理由：
∵AC=A1C,BC=B1C
又AC=BC
∴AA1=BB1
∴四边形AB1A1B是矩形
练习册系列答案
相关题目
19、如图，在正方形网格中，△ABC的三个顶点都在格点上，结合所给的平面直角坐标系解答下列问题：
如图，∠AOB放置在正方形网格中，则cos∠AOB的值为（ ）
在正方形网格中，△ABC在网格中的位置如图，则cosB的值为（ ）
