题目内容
12.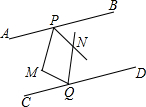 如图,M为两条平行线AB、CD之间的一点,P、Q分别在直线AB、CD上,∠BPM、∠DQM的平分线交于点N,若∠M=100°,则∠PNQ的度数为( )
如图,M为两条平行线AB、CD之间的一点,P、Q分别在直线AB、CD上,∠BPM、∠DQM的平分线交于点N,若∠M=100°,则∠PNQ的度数为( )| A. | 100° | B. | 110° | C. | 120° | D. | 130° |
分析 过点N作FN∥AB,过点M作ME∥AB,再由平行线的性质得出∠BPM+∠DQM的度数,进而可得出∠APM+∠CQM的度数,由此可得出结论.
解答  解:过点N作FN∥AB,过点M作ME∥AB,
解:过点N作FN∥AB,过点M作ME∥AB,
∵AB∥CD,
∴FN∥AB∥ME∥AB,
∵∠M=100°,
∴∠BPM+∠DQM=360°-100°=260°,
∴∠APM+∠CQM=360°-260°=100°.
∵∠BPM、∠DQM的平分线交于点N,
∴∠MPN+∠MQN=$\frac{1}{2}$(∠BPM+∠DQM)=130°,
∴∠APN+∠CQN=100°+130°=230°,
∴∠PNQ=360°-230°=130°.
故选D.
点评 本题考查的是平行线的性质,根据题意作出辅助线,构造出平行线是解答此题的关键.

练习册系列答案
相关题目
4.下面的数中,比-2小的数的是( )
| A. | 2 | B. | -1 | C. | 0 | D. | -3 |
1.小雨将平面直角坐标系中的三角形ABC进行平移,得到三角形A′B′C′,已知点A(2,-1)的对应点A′的坐标为(a,-4),点B(5,-2)的对应点B′的坐标为(3,b),则点C(a,b)的对应点C′的坐标为( )
| A. | (3,-4) | B. | (-2,-8) | C. | (0,-5) | D. | 无法确定 |
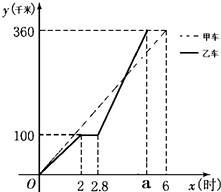 甲、乙两车同时出发从A地前往B地,乙行驶途中有一次停车修理,修好后乙车的行驶速度是原来的2倍.两车距离A地的路程y(千米)与行驶时间x(时)的函数图象如图所示.
甲、乙两车同时出发从A地前往B地,乙行驶途中有一次停车修理,修好后乙车的行驶速度是原来的2倍.两车距离A地的路程y(千米)与行驶时间x(时)的函数图象如图所示.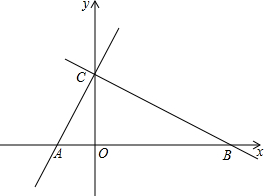 如图,直线y=-$\frac{\sqrt{3}}{3}$x+3和x轴、y轴的交点分别为B,C,点A的坐标是(-$\sqrt{3}$,0),∠ABC=30°,若动点M从B点出发沿BC运动,运动的速度为每秒1个单位长度,当点M运动到C点时停止运动,设点M运动t秒时,△ABM的面积为S.
如图,直线y=-$\frac{\sqrt{3}}{3}$x+3和x轴、y轴的交点分别为B,C,点A的坐标是(-$\sqrt{3}$,0),∠ABC=30°,若动点M从B点出发沿BC运动,运动的速度为每秒1个单位长度,当点M运动到C点时停止运动,设点M运动t秒时,△ABM的面积为S.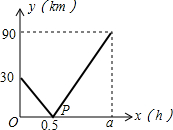 在一条直线上依次有A、B、C三个海岛,某海巡船从A岛出发沿直线匀速经过B岛驶向C岛,执行海巡任务,最终达到C岛.设该海巡船行驶x(h)后,与B港的距离为y(km),且y与x的函数关系如图所示,已知P点的坐标为(0.5,0),在B岛有一个不间断发射信号的信号发射台,发射的信号覆盖半径为24km,则该海巡船能接受到该信号的持续时间有0.8小时.
在一条直线上依次有A、B、C三个海岛,某海巡船从A岛出发沿直线匀速经过B岛驶向C岛,执行海巡任务,最终达到C岛.设该海巡船行驶x(h)后,与B港的距离为y(km),且y与x的函数关系如图所示,已知P点的坐标为(0.5,0),在B岛有一个不间断发射信号的信号发射台,发射的信号覆盖半径为24km,则该海巡船能接受到该信号的持续时间有0.8小时.