题目内容
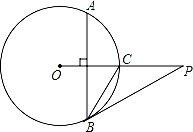
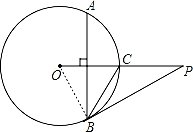
如图,已知点P是⊙O外一点,PO交圆O于点C,OC=2,AB⊥OC,劣弧AB的度数为120°,连接PB.
(1)求征:OC=BC;
(2)当PB的长是多少时,PB是⊙O的切线?写出证明过程.
【考点】切线的判定.
【专题】证明题.
【分析】(1)根据垂径定理得OC平分劣弧AB,则劣弧AC和劣弧BC的度数为60°,则利用圆心角的度数等于它所对弧的度数得∠COB=60°,连接OB,如图,易证得△OBC是等边三角形,所以BC=OC;
(2)由△OBC是等边三角形,则BC=OC=OB=2,∠BOP=60°,所以当∠P=30°时,∠OBP=90°,则根据切线的判定定理可判断此时PB是⊙O的切线,利用含30度的直角三角形三边的关系得到PB=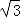 OB=2
OB=2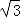 ,即当PB=2
,即当PB=2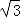 时,PB是⊙O的切线.
时,PB是⊙O的切线.
【解答】(1)证明:∵AB⊥OC,
∴OC平分劣弧AB,
∵劣弧AB的度数为120°,
∴劣弧AC和劣弧BC的度数为60°,
即∠COB=60°,
连接OB,如图,
∵OC=OB,∠COB=60°,
∴△OBC是等边三角形,
∴BC=OC;
(2)当PB=2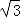 时,PB是⊙O的切线.
时,PB是⊙O的切线.
证明如下:∵△OBC是等边三角形,
∴BC=OC=OB=2,∠BOP=60°,
当∠P=30°时,∠OBP=90°,
∴OB⊥PB,
∴此时PB是⊙O的切线,
∴PB=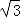 OB=2
OB=2 ..
..
【点评】本题考查了切线的判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线.记住含30度的直角三角形三边的关系.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
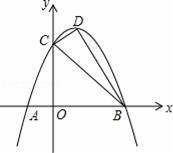

 的图象与一次函数y=2x+1的图象的一个交点是(1,k),则反比例函数的解析式是 .
的图象与一次函数y=2x+1的图象的一个交点是(1,k),则反比例函数的解析式是 . ,其中
,其中 ,
, .
.


 米,则这个坡面的坡度为( )
米,则这个坡面的坡度为( )