题目内容
 在平面直角坐标系中,直线y=x-4分别与x轴、y轴交于A、B两点,点C是第四象限内一点,且∠ACB=90°,则点C的横坐标m的取值范围是
在平面直角坐标系中,直线y=x-4分别与x轴、y轴交于A、B两点,点C是第四象限内一点,且∠ACB=90°,则点C的横坐标m的取值范围是考点:圆周角定理,一次函数图象上点的坐标特征
专题:
分析:以AB为直径作圆,找到点C的位置,求出点C的横坐标的最小值,再根据C在第四象限求出C的最大值.
解答: 解:如图,作CD∥x轴交⊙D于C,连接AC、BC.
解:如图,作CD∥x轴交⊙D于C,连接AC、BC.
∵直线y=x-4分别与x轴、y轴交于A、B两点,
∴A(4,0),B(0,-4).
AB=
=4
,
∴DC=
AB=
×4
=2
,
∵D点横坐标为
=2,
∴C点横坐标为2-2
,
∴横坐标m的取值范围是2-2
≤m<0.
故答案为2-2
≤m<0.
 解:如图,作CD∥x轴交⊙D于C,连接AC、BC.
解:如图,作CD∥x轴交⊙D于C,连接AC、BC.∵直线y=x-4分别与x轴、y轴交于A、B两点,
∴A(4,0),B(0,-4).
AB=
| 42+42 |
| 2 |
∴DC=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
∵D点横坐标为
| 0+4 |
| 2 |
∴C点横坐标为2-2
| 2 |
∴横坐标m的取值范围是2-2
| 2 |
故答案为2-2
| 2 |
点评:本题考查了圆周角定理和一次函数图象上点的坐标特征及直径所对的圆周角是90度,要注意画出图形.

练习册系列答案
相关题目
我国以2011年11月1日零时为标准时点进行了第六次全国人口普查,普查得到全国总人口为1370536875人,该数用科学记数法表示并保留三位有效数字为( )
| A、1.37×109 |
| B、13.7×108 |
| C、1.4×109 |
| D、13.7 亿 |
来自某综合市场财务部的报告表明,商场2014年1-4月份的投资总额一共是2017万元,商场2014年第一季度每月利润统计图和2014年1-4月份利润率统计图如下(利润率=利润÷投资金额):

根据以上信息,下列判断不正确的是( )

根据以上信息,下列判断不正确的是( )
| A、商场2014年第一季度中3月份投资金额最多 |
| B、商场2014年第一季度中2月份投资金额最少 |
| C、商场2014年4月份利润比2月份的利润高 |
| D、商场四个月的利润所组成的一组数据的中位数是124 |
如果4x=3y,则
=( )
| 2x+y |
| 2x-y |
A、
| ||
| B、5 | ||
C、
| ||
D、
|
 如图的数轴上A、B两点分别对应实数a、b,则|a|与|b|的大小关系为|a|
如图的数轴上A、B两点分别对应实数a、b,则|a|与|b|的大小关系为|a|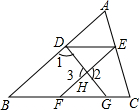 完成下面的证明过程.
完成下面的证明过程.