题目内容
6. 如图,直线y=x+4与双曲线y=-$\frac{3}{x}$相交于A、B两点,点P是y轴上的一个动点,当PA+PB的值最小时,点P的坐标为( )
如图,直线y=x+4与双曲线y=-$\frac{3}{x}$相交于A、B两点,点P是y轴上的一个动点,当PA+PB的值最小时,点P的坐标为( )| A. | (0,$\frac{5}{3}$) | B. | (0,$\frac{5}{2}$) | C. | (0,-$\frac{5}{3}$) | D. | (0,-$\frac{5}{2}$) |
分析 根据轴对称-最短路径全等点P,解方程组求出A、B的坐标,得到A′的坐标,求出直线BA′的解析式,计算即可.
解答 解: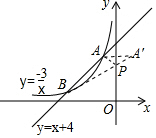 作点A关于y轴的对称点A′,连接A′B交y轴于P,
作点A关于y轴的对称点A′,连接A′B交y轴于P,
则点P即为所求,
$\left\{\begin{array}{l}{y=x+4}\\{y=-\frac{3}{x}}\end{array}\right.$,
解得,$\left\{\begin{array}{l}{{x}_{1}=-1}\\{{y}_{1}=3}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{2}=-3}\\{{y}_{2}=1}\end{array}\right.$,
则点A的坐标为(-1,3),点B的坐标为(-3,1),
∴点A′的坐标为(1,3),
设直线BA′的解析式为:y=kx+b,
$\left\{\begin{array}{l}{-3k+b=1}\\{k+b=3}\end{array}\right.$,
解得,$\left\{\begin{array}{l}{k=\frac{1}{2}}\\{b=\frac{5}{2}}\end{array}\right.$,
∴直线BA′的解析式为:y=$\frac{1}{2}$x+$\frac{5}{2}$,
当x=0时,y=$\frac{5}{2}$,
∴点P的坐标为(0,$\frac{5}{2}$),
故选:B.
点评 本题考查的是一次函数的解析式、反比例函数解析式、反比例函数与一次函数的交点问题以及轴对称-最短路径问题,掌握待定系数法求函数解析式的一般步骤是解题的关键.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
1.我国是个缺水国家,目前可利用淡水资源总量仅约为899 000乙亿米3,其中数据899 000用科学记数法表示为( )
| A. | 8.99×104 | B. | 0.899×106 | C. | 899×103 | D. | 8.99×105 |
18.甲、乙两人从同一地点出发,同向而行.甲骑自行车,乙步行.如果乙先行12千米,甲用1小时就追上乙;如果乙先走1小时,那么甲只用$\frac{1}{2}$小时就追上乙,则甲的速度是( )
| A. | 6千米/小时 | B. | 12千米/小时 | C. | 18千米/小时 | D. | 36千米/小时 |
15.若(3x2y-2xy2)÷M=xy,则代数式M为( )
| A. | 3x+2y | B. | 3x-2y | C. | 6xy | D. | x-y |
16.甲、乙两名运动员在相同的条件下,各射击10次,经过计算,甲、乙两人成绩的平均数均是9.5环,甲的成绩的方差是0.125,乙的成绩的方差是0.85,那么这10次射击中,甲、乙成绩的稳定情况是( )
| A. | 甲较为稳定 | B. | 乙较为稳定 | ||
| C. | 两个人成绩一样稳定 | D. | 不能确定 |
 如图,AC=AD,BC=BD,试说明∠C=∠D.
如图,AC=AD,BC=BD,试说明∠C=∠D.