题目内容
20.△ABC中,∠ACB=90°,CD是斜边AB上的高,AB=4cm,AC=2$\sqrt{3}$cm,则AD=3cm.分析 根据已知条件证出△ACB∽△ADC,得出$\frac{AC}{AD}$=$\frac{AB}{AC}$,再把AB=4cm,AC=2$\sqrt{3}$cm代入进行计算,即可得出AD的值.
解答 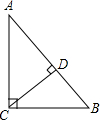 解:∵CD⊥AB,
解:∵CD⊥AB,
∴∠CDA=90°,
∵∠ACB=90°,
∴△ACB∽△ADC,
∴$\frac{AC}{AD}$=$\frac{AB}{AC}$,
∵AB=4cm,AC=2$\sqrt{3}$cm,
∴$\frac{2\sqrt{3}}{AD}$=$\frac{4}{2\sqrt{3}}$,
∴AD=3cm.
故答案为:3.
点评 本题考查了解直角三角形,用到的知识点是相似三角形的判定和性质、勾股定理,解题的关键是证明△ACB∽△ADC,求出AD.

练习册系列答案
相关题目
9.若X=2$\sqrt{2}$+$\sqrt{20}$,Y=3$\sqrt{3}$+$\sqrt{7}$,Z=$\sqrt{6}$+2$\sqrt{7}$,则( )
| A. | X最小 | B. | Y最小 | C. | Z最小 | D. | X、Y、Z一样大 |
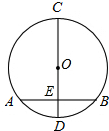 如图,在⊙O中,直径CD垂直于弦AB于点E.
如图,在⊙O中,直径CD垂直于弦AB于点E.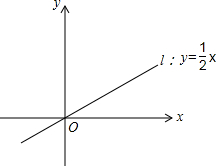 如图,直线l:y=$\frac{1}{2}$x,若直线上有一点A,A在第一象限,且OA=$\sqrt{5}$.
如图,直线l:y=$\frac{1}{2}$x,若直线上有一点A,A在第一象限,且OA=$\sqrt{5}$. 如图,点C、O、D在同一直线上,∠AOB=90°,∠BOD=25°,求∠AOC的度数.
如图,点C、O、D在同一直线上,∠AOB=90°,∠BOD=25°,求∠AOC的度数.