题目内容
10.若方程(m-1)x2+$\sqrt{m}$x-2=0是关于x的一元二次方程,则m的取值范围是( )| A. | m=0 | B. | m≠1 | C. | m≥0且m≠1 | D. | m为任意实数 |
分析 根据一元二次方程的定义:未知数的最高次数是2;二次项系数不为0;是整式方程;含有一个未知数.由这四个条件对四个选项进行验证,满足这四个条件者为正确答案.
解答 解:方程(m-1)x2+$\sqrt{m}$x-2=0是关于x的一元二次方程,得
m-1≠0,且m≥0
解得m≥0且m≠1,
故选:C.
点评 本题考查了一元二次方程的概念,判断一个方程是否是一元二次方程,首先要看是否是整式方程,然后看化简后是否是只含有一个未知数且未知数的最高次数是2.

练习册系列答案
相关题目
1.若△MNP≌△NMQ,且MN=8cm,NP=7cm,PM=6cm,则MQ的长为( )
| A. | 5cm | B. | 6cm | C. | 7cm | D. | 8cm |
18.抛物线y=x2不具有的性质是( )
| A. | 对称轴是y轴 | B. | 开口向上 | ||
| C. | 当x<0时,y随x的增大而增大 | D. | 顶点坐标是(0,0) |
15.某商场经营某种品牌的玩具,购进时的单价是30元,根据市场调查:在一段时间内,销售单价是40元时,销售量是600件,而销售单价每涨1元,就会少售出10件玩具.
(1)不妨设该种品牌玩具的销售单价为x元(x>40),请你分别用含x的代数式来表示销售量(件)和销售该品牌玩具获得利润(元),并把化简后的结果填写在表格中:
(2)在(1)问条件下,若商场获得了10000元销售利润,试问该玩具销售单价x应定为多少元?
(3)在(1)问条件下,商场有可能获得13000元的销售利润吗?若可能,请求出该玩具销售单价;若不可能,请说明理由.
(1)不妨设该种品牌玩具的销售单价为x元(x>40),请你分别用含x的代数式来表示销售量(件)和销售该品牌玩具获得利润(元),并把化简后的结果填写在表格中:
| 销售单价(元) | x |
| 销售量(件) | 1000-10x |
| 销售玩具获得利润(元) | -10x2+1300x-30000 |
(3)在(1)问条件下,商场有可能获得13000元的销售利润吗?若可能,请求出该玩具销售单价;若不可能,请说明理由.
19.若不等式组$\left\{\begin{array}{l}x>7a+2\\ x<4a-7\end{array}\right.$无解,则a的取值范围是( )
| A. | a≥-3 | B. | a>-3 | C. | a≤-3 | D. | a<-3 |
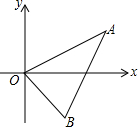 如图,已知A (4,2),B(2,-2),以点O为位似中心,按位似比1:2把△ABO缩小,则点A的对应点A′的坐标为(2,1)或(-2,-1).
如图,已知A (4,2),B(2,-2),以点O为位似中心,按位似比1:2把△ABO缩小,则点A的对应点A′的坐标为(2,1)或(-2,-1).