题目内容
已知a3±b3=(a±b)(a2±ab+b2),如果一列数a1,a2,…满足对任意的正整数n都有 ,则
,则 的值为
的值为
- A.
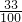
- B.

- C.

- D.

A
分析:令n=1、2、3…,求出a1,a2,…的值,在表示出a2-1,a3-1,…从而得出规律,再提取 后利用拆项法解答.
后利用拆项法解答.
解答:根据题意,当n=1时,a1=13=1,
当n=2时,a1+a2=23,a2=23-1=7,
所以a2-1=7-1=6=3×(1×2),
当n=3时,a1+a2+a3=33,a3=33-23=19,
所以a3-1=19-1=18=3×(2×3),
当n=4时,a1+a2+a3+a4=43,a4=43-33=37,
所以a4-1=37-1=36=3×(3×4),
…
a100=1003-993
=(100-99)×(1002+100×99+992)
=1002+100×(100-1)+(100-1)2
=1002+1002-100+1002-200+1
=3×1002-300+1,
所以a100-1=3×1002-100+1-1=100×(300-3)=100×297=3×(99×100),
 +
+ +…+
+…+
= +
+ +
+ +…+
+…+
= (
( -
- +
+ -
- +
+ -
- +…+
+…+ -
- )
)
= ×(1-
×(1- )
)
= ×
×
=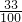 .
.
故选A.
点评:本题考查了分式的混合运算,令n=1、2、3…,分别求出a2-1,a3-1,a4-1,…,a100-1并发现规律是解题的关键.
分析:令n=1、2、3…,求出a1,a2,…的值,在表示出a2-1,a3-1,…从而得出规律,再提取
 后利用拆项法解答.
后利用拆项法解答.解答:根据题意,当n=1时,a1=13=1,
当n=2时,a1+a2=23,a2=23-1=7,
所以a2-1=7-1=6=3×(1×2),
当n=3时,a1+a2+a3=33,a3=33-23=19,
所以a3-1=19-1=18=3×(2×3),
当n=4时,a1+a2+a3+a4=43,a4=43-33=37,
所以a4-1=37-1=36=3×(3×4),
…
a100=1003-993
=(100-99)×(1002+100×99+992)
=1002+100×(100-1)+(100-1)2
=1002+1002-100+1002-200+1
=3×1002-300+1,
所以a100-1=3×1002-100+1-1=100×(300-3)=100×297=3×(99×100),
 +
+ +…+
+…+
=
 +
+ +
+ +…+
+…+
=
 (
( -
- +
+ -
- +
+ -
- +…+
+…+ -
- )
)=
 ×(1-
×(1- )
)=
 ×
×
=
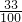 .
.故选A.
点评:本题考查了分式的混合运算,令n=1、2、3…,分别求出a2-1,a3-1,a4-1,…,a100-1并发现规律是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目