Question

4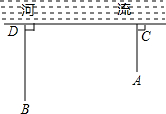．如图，草原上，一牧童在A处放马，牧童家在B处，A、B处距河岸的距离AC，BD的长分别为500m和700m，且CD=500m，天黑前牧童从A点将马牵到河边去饮水后，再赶回家，牧童将马牵到河边什么地方饮水，才能使走过的路程最短？牧童最少要走多少m？

Answer 1

分析 将此题转化为轴对称问题，作出A点关于河岸的对称点A′，根据两点之间线段最短得出BA′的长即为牧童要走的最短路程，利用勾股定理解答即可．

解答 解：作A点关于河岸的对称点A′，连接BA′交河岸与P，连接A′B′，则BB′=BD+DB′=1200，
则PB+PA=PB+PA′=BA′最短，故牧童应将马赶到河边的P地点．
作DB′=CA′，且DB′⊥CD，
∵DB′=CA′，DB′⊥CD，BB′∥A′A，
∴四边形A′B′BA是矩形，
∴B'A'=CD，
在Rt△BB′A′中，
BA′=$\sqrt{120{0}^{2}+50{0}^{2}}$=1300（m）．
故牧童至少要走1300米．

点评 此题考查了轴对称--最短路径问题在生活中的应用，要将轴对称的性质和勾股定理灵活应用，体现了数学在解决简单生活问题时的作用．