题目内容
直线y=kx(k>0)与双曲线y=
交于A(x1,y1),B(x2,y2)两点,则2x1y2-5x2y1的值等于 .
| 4 |
| x |
考点:反比例函数与一次函数的交点问题
专题:
分析:把直线y=kx(k>0)与双曲线y=
联立求解,再代入2x1y2-5x2y1求值.
| 4 |
| x |
解答:解:∵直线y=kx(k>0)与双曲线y=
交于A(x1,y1),B(x2,y2)两点,
∴
,
解得
,
,
∴2x1y2-5x2y1=2(-
)•2
-5
•(-2
)=-8+20=12.
故答案为:12.
| 4 |
| x |
∴
|
解得
|
|
∴2x1y2-5x2y1=2(-
2
| ||
| k |
| k |
2
| ||
| k |
| k |
故答案为:12.
点评:本题主要考查了反比例函数与一次函数的交点问题,解题的关键是把两个函数关系式联立成方程组并能正确求解.

练习册系列答案
 巧学巧练系列答案
巧学巧练系列答案 课课练江苏系列答案
课课练江苏系列答案
相关题目
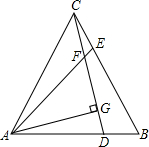 如图,在等边三角形ABC中,D、E分别为AB、BC上的点,且BD=CE,AE、CD相交于点F,AG⊥CD,垂足为G.求证:
如图,在等边三角形ABC中,D、E分别为AB、BC上的点,且BD=CE,AE、CD相交于点F,AG⊥CD,垂足为G.求证: 如图,菱形ABCD中,若BD=24,AC=10,则AB的长等于
如图,菱形ABCD中,若BD=24,AC=10,则AB的长等于 如图,在正方形ABCD中,AC、BD相交于点O,点E是AB延长线上一点,点F是边AD上一点,BE=DF,连接EF,分别交AC、BD于点H、G,连接AG.若AB=3,FH:HE=1:2,则线段AG的长为
如图,在正方形ABCD中,AC、BD相交于点O,点E是AB延长线上一点,点F是边AD上一点,BE=DF,连接EF,分别交AC、BD于点H、G,连接AG.若AB=3,FH:HE=1:2,则线段AG的长为 已知抛物线y=a(x-3)2+
已知抛物线y=a(x-3)2+